Производная логарифма по основанию a
![Rendered by QuickLaTeX.com \[ \left( \log _{a} x \right)' = \frac{1}{x \ln a} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-bbd83511ff56e92657f66326a796e066_l3.png)
Данная формула справедлива для любого ![]() .
.
Заметим, что если основание логарифма ![]() , то получаем логарифм натуральный и его производная равна
, то получаем логарифм натуральный и его производная равна
![]()
Примеры решения задач по теме «Производная логарифма»
| Задание | Найти производную функции |
| Решение | Искомая производная
Производную произведения найдем по формуле: Тогда в нашем случае для Производная независимой переменной производная логарифма: Итак, имеем: |
| Ответ | 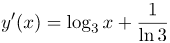 |
| Задание | Найти производную функции |
| Решение | Производная заданной функции
Задан десятичный логарифм, то есть его основание Найдем производную от подлогарифмической функции. Константу выносим за знак производной: Производная независимой переменной Таким образом, окончательно имеем: |
| Ответ | 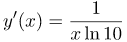 |











