Производная котангенса
![Rendered by QuickLaTeX.com \[ \left( \text{ctg} x \right)' = -\frac{1}{\sin^{2} x} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-a7a543951746b948eb24cbb4fd35ceeb_l3.png)
Заметим, что эта формула легко получается из того факта, что ![]() , а также из формулы дифференцирования частного:
, а также из формулы дифференцирования частного:
![]()
с учетом того, что ![]() .
.
Если аргумент тангенса есть функция более сложная, чем просто «икс», то есть является сложной функцией, то надо умножить еще на производную аргумента. В этом случае формула производной принимает вид:
![]()
Примеры решения задач по теме «Производная котангенса»
| Задание | Найти производную функции |
| Решение | Искомая производная
Производная от корня равна единице деленной на два таких же корня и все это мы еще умножаем на производную от подкоренного выражения, так как там стоит функция более сложная, чем просто Производная котангенс икс равна минус единице деленной на минус синус квадрат икс, то есть: |
| Ответ | 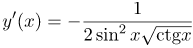 |
| Задание | Найти производную функции |
| Решение | Производная заданной функции равна:
Производная от котангенса равна минус единице деленной на синус в квадрате того же аргумента. Так как заданная функция является сложной (аргумент котангенса отличен от просто Производная от корня равна единице деленной на два таких же корня. И так как подкоренное выражение отлично от Производная суммы равна сумме производных: Производная от независимой переменной |
| Ответ | 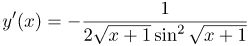 |











