Производная арксинуса
![Rendered by QuickLaTeX.com \[ \left( \arcsin x \right)' = \frac{1}{\sqrt{1-x^{2}}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9d00997fe532b56ac54f5b2f1d98b1f0_l3.png)
Функция ![]() является обратной к функции
является обратной к функции ![]() и также является нечетной.
и также является нечетной.
Если аргумент арксинуса есть сложной функцией (то есть там стоит выражение более сложное, чем просто ![]() ), то формула для производной принимает вид:
), то формула для производной принимает вид:
![]()
Примеры решения задач по теме «Производная арксинуса»
| Задание | Найти производную функции |
| Решение | Производная заданной функции равна:
Производную арксинуса находим по формуле и так как аргумент отличен от просто Производна разности равна разности производных: Производная Тогда окончательно имеем: |
| Ответ | 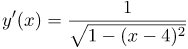 |
| Задание | Продифференцировать функцию |
| Решение | Искомая производная
Вначале находим производную от корня: Находим далее производную от арксинуса: |
| Ответ | 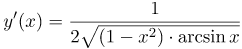 |











