Производная арккосинуса
![Rendered by QuickLaTeX.com \[ \left( \arccos x \right)' = -\frac{1}{\sqrt{1-x^{2}}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1d8a7b70f27da22c014f0f0e1f979351_l3.png)
Как можно отметить, производная арккосинуса отличается от производной арксинуса только знаком.
Функция ![]() является обратной к функции
является обратной к функции ![]() , но в отличии от второй является функцией общего вида.
, но в отличии от второй является функцией общего вида.
Примеры решения задач по теме «Производная арккосинуса»
| Задание | Найти производную функции |
| Решение | Искомая производная
Находим производную арккосинуса. Так как аргумент отличен от Производная от корня равна единице деленной на два таких же корня, то есть имеем: |
| Ответ | 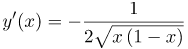 |
| Задание | Найти производную функции |
| Решение | Искомая производная равна:
Находим производную арккосинуса и домножаем на производную от его аргумента, так как он отличен от Производная разности равна разности производных: Производную от Производная шестерки, как константы, равна нулю: Итак, окончательно имеем: |
| Ответ | 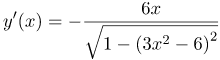 |






![Rendered by QuickLaTeX.com \[ y'(x) = \left( \arccos \sqrt{x} \right)' = -\frac{1}{\sqrt{1-\left( \sqrt{x} \right)^{2}}} \cdot \left( \sqrt{x} \right)' = -\frac{1}{\sqrt{1-x}} \cdot \left( \sqrt{x} \right)' \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-75c3f010cfe990baf33a3c124023c809_l3.png)
![Rendered by QuickLaTeX.com \[ y'(x) = -\frac{1}{\sqrt{1-\left( 3x^{2}-6 \right)^{2}}} \cdot \left( 3x^{2}-6 \right)' \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6c7c1ac8f008c7b2aa85b8c1aff084f9_l3.png)
![Rendered by QuickLaTeX.com \[ y'(x) = -\frac{1}{\sqrt{1-\left( 3x^{2}-6 \right)^{2}}} \cdot \left[ \left( 3x^{2} \right)' - \left( 6 \right)' \right] \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c88c824d293b32d10383945ae09797b6_l3.png)
![Rendered by QuickLaTeX.com \[ y'(x) = -\frac{1}{\sqrt{1-\left( 3x^{2}-6 \right)^{2}}} \cdot \left( 6x-0 \right) = -\frac{6x}{\sqrt{1-\left( 3x^{2}-6 \right)^{2}}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-0843255819338702cdc83b792f3e15c5_l3.png)





