Формула суммы арифметической прогрессии
ОПРЕДЕЛЕНИЕ
Последовательность чисел вида 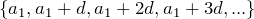 называется арифметической прогрессией с первым членом
называется арифметической прогрессией с первым членом 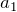 и разностью
и разностью 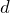 .
.
Сумму первых ![]() членов арифметической прогрессии можно вычислить по формуле:
членов арифметической прогрессии можно вычислить по формуле:
![]()
Если же известен только первый член прогрессии ![]() и разность
и разность ![]() , то можно воспользоваться другой формулой:
, то можно воспользоваться другой формулой:
![]()
Примеры решения задач
ПРИМЕР 1
| Задание | Вычислить сумму первых восьми членов арифметической прогрессии, если |
| Решение | Если известны первый член арифметической прогрессии и ее разность, то сумму первых n членов можно найти по формуле:
Найдем сумму первых восьми членов заданной прогрессии |
| Ответ |
ПРИМЕР 2
| Задание | Найти сумму |
| Решение | В заданной сумме каждое слагаемое является членом арифметической прогрессии с |
| Ответ |











