Точки разрыва функции

ОПРЕДЕЛЕНИЕ

Если в точке $x=a$ функция $y=f\left( x \right)$ не является непрерывной, то эта точка называется точкой разрыва функции.

Классификация точек разрыва функции

Точка $x=a$ называется точкой устранимого разрыва функции $y=f\left( x \right)$ , если в этой точке односторонние пределы конечны и равны между собой, но не равны значению функции в этой точке; или функция в точке $x=a$ не определена (рис. 1).

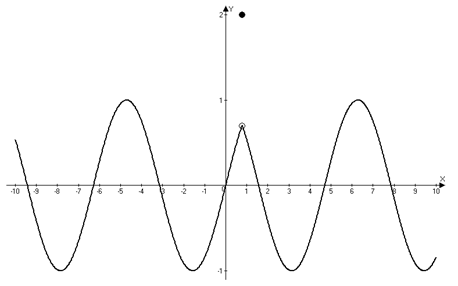
Рис. 1

$f\left( a+0 \right)=f\left( a-0 \right)\ne f\left( a \right)\vee \not{\exists }\,f\left( a \right)$

Точка $x=a$ называется точкой разрыва первого рода функции $y=f\left( x \right)$ , если в этой точке односторонние пределы конечны и не равны между собой (рис. 2).

$f\left( a+0 \right)\ne f\left( a-0 \right)$

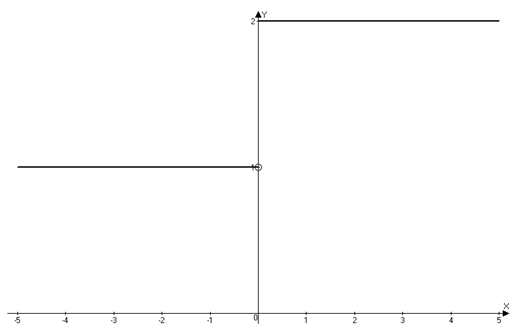
Рис. 2

Модуль разности значений односторонних пределов $\left| f\left( a+0 \right)-f\left( a-0 \right) \right|$ называется скачком функции.

Пример. На рисунке 2 скачок функции равен $\left| 2-1 \right|=2$

Точка $x=a$ называется точкой разрыва второго рода функции $y=f\left( x \right)$ , если в этой точке, по крайней мере, один из односторонних пределов равен бесконечности или не существует (рис. 3).

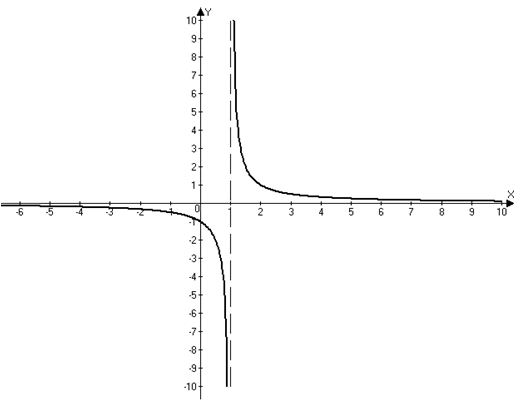
Рис. 3

Примеры решения задач

ПРИМЕР

Задание

Исследовать функцию на непрерывность и классифицировать точки разрыва.

$y=\frac{5x-12}{{{x}^{2}}+11x+30}$

Решение

Функция является непрерывной как отношение двух непрерывных функций (многочленов), разрыв может быть лишь в точках, в которых знаменатель обращается в нуль, то есть

${{x}^{2}}+11x+30=0\Rightarrow {{x}_{1}}=-5,\ {{x}_{2}}=-6$

Итак, если разрыв есть, то он может быть лишь в точках ${{x}_{1}}=-5,\ {{x}_{2}}=-6$ . Исследуем функцию на непрерывность в этих точках. Для этого найдем односторонние пределы:

$f\left( -5-0 \right)=\underset{x\to -5-0}{\mathop{\lim }}\,\frac{5x-12}{{{x}^{2}}+11x+30}=$

$\left[ \frac{5\cdot \left( -5-0 \right)-12}{{{\left( -5-0 \right)}^{2}}+11\cdot \left( -5-0 \right)+30}=\frac{-37}{25-55-0+30}=\frac{-37}{-0} \right]=+\infty$

аналогично

$f\left( -5+0 \right)=\underset{x\to -5+0}{\mathop{\lim }}\,\frac{5x-12}{{{x}^{2}}+11x+30}=\left[ \frac{-37}{+0} \right]=-\infty$

Поскольку односторонние пределы бесконечны, то в точке ${{x}_{1}}=-5$ функция имеет разрыв второго рода.

Аналогично для второй точки ${{x}_{2}}=-6$ :

$f\left( -6-0 \right)=\underset{x\to -6-0}{\mathop{\lim }}\,\frac{5x-12}{{{x}^{2}}+11x+30}=-\infty ,$

$f\left( -6+0 \right)=\underset{x\to -6+0}{\mathop{\lim }}\,\frac{5x-12}{{{x}^{2}}+11x+30}=+\infty$

то есть и точка ${{x}_{2}}=-6$ – точка разрыва другого роду.

Ответ

Функция терпит разрыв второго рода в точках ${{x}_{1}}=-5,\ {{x}_{2}}=-6$

ПРИМЕР

Задание

Исследовать функцию на непрерывность и сделать схематический чертеж.

$y=\left\{ \begin{matrix} & x^{2}-1,\ x\le 2, \\ & 7,\ x>2 \\ \end{matrix} \right.$

Решение

На каждом из промежутков $\left( -\infty ;\ 2 \right); \quad \left( 2;\ +\infty \right)$ функция задается элементарными функциями, поэтому разрыв может быть только лишь на концах промежутков, а именно в точке $x=2$ . Исследуем функцию на непрерывность в этой точке. Найдем односторонние пределы:

$f\left( 2-0 \right)=\underset{x\to 2-}{\mathop{\lim }}\,\left( {{x}^{2}}-1 \right)=3, \quad f\left( 2+0 \right)=\underset{x\to 2+}{\mathop{\lim }}\,7=7$

Так як $f\left( 2-0 \right)\ne f\left( 2+0 \right)$ , то точка $x=2$ является точкой разрыва первого рода.

Сделаем схематический чертеж (рис. 4).

Рис. 4

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Точки разрыва функции

Классификация точек разрыва функции

Примеры решения задач