Предел функции в точке

Определение предела функции в точке по Гейне

Это определение предела функции на языке последовательностей.

ОПРЕДЕЛЕНИЕ

Число $b$ называется пределом функции $y=f\left( x \right)$ при $x$ , стремящемся к $a$ (или, что тоже самое, в точке $a$ ), если для любой последовательности $\left\{ {{x}_{n}} \right\}$ , сходящейся к $a$ ( ${{x}_{n}}\ne a\ \forall n$ ), последовательность соответствующих значений функции $\left\{ f\left( {{x}_{n}} \right) \right\}$ сходится к $b$ :

$\underset{x\to a}{\mathop{\lim }}\,f\left( x \right)=b:\forall \left\{ {{x}_{n}} \right\}\subset D\left[ f \right]:\left\{ {{x}_{n}} \right\}\underset{n\to \infty }{\mathop{\to }}\,a\Rightarrow \left\{ f\left( {{x}_{n}} \right) \right\}\underset{n\to \infty }{\mathop{\to }}\,b$

ПРИМЕР

Задание

Доказать равенство $\underset{x\to \infty }{\mathop{\lim }}\,\frac{1}{x}=0$ , пользуясь определением предела функции по Гейне.

Доказательство

Согласно определению предела функции по Гейне:

$\underset{x\to \infty }{\mathop{\lim }}\,\frac{1}{x}=0:\forall \left\{ {{x}_{n}} \right\}\subset D\left[ f \right]:\underset{n\to \infty }{\mathop{\lim }}\,{{x}_{n}}=\infty \Rightarrow \underset{n\to \infty }{\mathop{\lim }}\,f\left( {{x}_{n}} \right)=0$

Пусть $\underset{n\to \infty }{\mathop{\lim }}\,{{x}_{n}}=\infty$ , докажем, что $\underset{n\to \infty }{\mathop{\lim }}\,f\left( {{x}_{n}} \right)=0$ . Предел значений функции

$\underset{n\to \infty }{\mathop{\lim }}\,f\left( {{x}_{n}} \right)=\underset{n\to \infty }{\mathop{\lim }}\,\frac{1}{{{x}_{n}}}$

Поскольку последовательность $\left\{ {{x}_{n}} \right\}$ является бесконечно большой (ее предел равен бесконечности), то последовательность $\left\{ \frac{1}{{{x}_{n}}} \right\}$ – бесконечно малая, а это означает, что ее предел равен нулю. Тогда

$\underset{n\to \infty }{\mathop{\lim }}\,f\left( {{x}_{n}} \right)=\underset{n\to \infty }{\mathop{\lim }}\,\frac{1}{{{x}_{n}}}=0$

Что и требовалось доказать.

Определение предела функции в точке по Коши

Это определение предела функции на языке « $\varepsilon$ — $\delta$ ».

ОПРЕДЕЛЕНИЕ

Число $b$ называется пределом функции $y=f\left( x \right)$ при $x$ , стремящемся к $a$ , если для любого положительного числа $\varepsilon$ существует такое положительное число $\delta$ , что при всех $x\ne a$ таких, что $\left| x-a \right|<\delta$ выполняется неравенство $\left| f\left( x \right)-a \right|<\varepsilon$ :

$\underset{x\to a}{\mathop{\lim }}\,f\left( x \right)=b:\forall \varepsilon >0\ \exists \delta >0:\forall x\in \left( a-\delta ;\ a+\delta \right)\ \bigcap D\left[ f \right]:0<\left| x-a \right|<\delta \Rightarrow \left| f\left( x \right)-b \right|<\varepsilon$

ПРИМЕР

Задание

Доказать равенство $\underset{x\to 3}{\mathop{\lim }}\,\left( {{x}^{2}}-1 \right)=8$ , пользуясь определением предела функции по Коши.

Доказательство

Согласно определению предела функции по Коши, имеем, что

$\underset{x\to 3}{\mathop{\lim }}\,\left( {{x}^{2}}-1 \right)=8:\forall \varepsilon >0\ \exists \delta =\delta \left( \varepsilon \right)>0:\forall x\in D\left[ f \right]:0<\left| x-3 \right|<\delta \Rightarrow$

$\Rightarrow \left| \left( {{x}^{2}}-1 \right)-8 \right|<\varepsilon$

То есть необходимо найти такое положительное $\delta$ , которое будет удовлетворять выше приведенным условиям.

Преобразуем последний модуль:

$\left| \left( {{x}^{2}}-1 \right)-8 \right|=\left| {{x}^{2}}-9 \right|=\left| \left( x-3 \right)\left( x+3 \right) \right|=\left| x-3 \right|\cdot \left| x+3 \right|=\left| x-3 \right|\cdot \left| \left( x-3 \right)+6 \right|$

Далее используем тот факт, что модуль суммы не превышает суммы модулей:

$\left| \left( {{x}^{2}}-1 \right)-8 \right|=\left| x-3 \right|\cdot \left| \left( x-3 \right)+6 \right|\le \left| x-3 \right|\cdot \left( \left| x-3 \right|+\left| 6 \right| \right)={{\left( \left| x-3 \right| \right)}^{2}}+6\left| x-3 \right|$

Выделим в полученном выражении полный квадрат:

$\left| \left( {{x}^{2}}-1 \right)-8 \right|\le {{\left( \left| x-3 \right| \right)}^{2}}+6\left| x-3 \right|={{\left( \left| x-3 \right| \right)}^{2}}+2\cdot \left| x-3 \right|\cdot 3+{{3}^{2}}-{{3}^{2}}=$

$={{\left( \left| x-3 \right|+3 \right)}^{2}}-9$

И по определению это должно быть меньше $\varepsilon$ :

$\left| \left( {{x}^{2}}-1 \right)-8 \right|\le {{\left( \left| x-3 \right|+3 \right)}^{2}}-9<\varepsilon$

Тогда

${{\left( \left| x-3 \right|+3 \right)}^{2}}<\varepsilon +9\Rightarrow \left| x-3 \right|+3<\sqrt{\varepsilon +9}\Rightarrow \left| x-3 \right|<\sqrt{\varepsilon +9}-3$

Итак, имеем, что с одной стороны

$\left| x-3 \right|<\sqrt{\varepsilon +9}-3$

а с другой (по определению) –

$\left| x-3 \right|<\delta$

Тогда делаем вывод, что в качестве $\delta$ можно взять

$\delta =\sqrt{\varepsilon +9}-3>0$

Таким образом:

$\forall \varepsilon >0\ \exists \delta \left( \varepsilon \right)=\sqrt{\varepsilon +9}-3>0:\forall x\in D\left[ f \right]:0<\left| x-3 \right|<\delta \Rightarrow \left| \left( {{x}^{2}}-1 \right)-8 \right|<\varepsilon$

Что и требовалось доказать.

ТЕОРЕМА

Определения предела функции в точке по Коши и по Гейне эквивалентны, то есть если число $b$ служит пределом по одному из них, то это верно и по второму.

Замечание 1. Из определения предела функции по Гейне следует, что функция не может иметь в точке двух разных пределов.

Замечание 2. Понятие предела функции в точке – локальное понятие: существование и значение предела полностью определяется значениями функции в как угодно малой окрестности этой точки.

Замечание 3. Геометрически существование предела функции в точке по Коши означает, что для любого числа $\varepsilon >0$ можно указать на координатной плоскости такой прямоугольник с основанием $2\delta >0$ и высотой $2\varepsilon$ , с точкой пересечения диагоналей $\left( a;\ b \right)$ , что все точки графика данной функции на интервале $\left( a-\delta ;\ a+\delta \right)$ , за исключением, быть может, точки $\left( a;\ f\left( a \right) \right)$ , лежат в этом прямоугольнике (рис. 1).

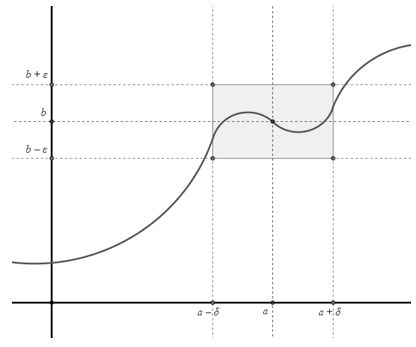
Рис. 1

Учитывая то, как будут раскрываться модули, а также тот факт, стремится $x$ слева или справа к значению $a$ , для записанных выше выражений можно построить следующую таблицу:

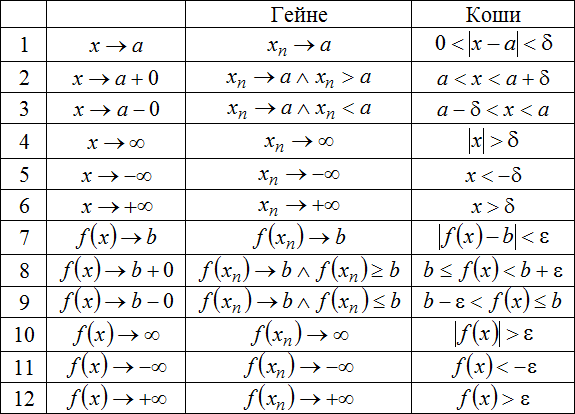
Во втором столбце записаны условия, накладываемые на переменную и функцию, а третий и четвертый столбцы соответствуют тому, как необходимо эти условия трактовать в определениях предела функции по Гейне и Коши соответственно.

Примеры решения задач

ПРИМЕР

Задание

Сформулировать с помощью неравенств утверждение $\underset{x\to \infty }{\mathop{\lim }}\,f\left( x \right)=b-0$ . Привести соответствующий пример.

Решение

Из таблицы берем строки 4 (соответствует $x\to \infty$ ) и 9 (соответствует $f\left( x \right)\to b-0$ ). Тогда утверждение для определения предела функции по Гейне с помощью неравенств запишется в виде:

$\underset{x\to \infty }{\mathop{\lim }}\,f\left( x \right)=b-0:\forall \left\{ {{x}_{n}} \right\}\subset D\left[ f \right]:{{x}_{n}}\underset{n\to \infty }{\mathop{\to }}\,\infty \Rightarrow \left\{ f\left( {{x}_{n}} \right) \right\}\underset{n\to \infty }{\mathop{\to }}\,b\wedge f\left( {{x}_{n}} \right)\le b$

Аналогично, для определения предела функции по Коши имеем:

$\underset{x\to \infty }{\mathop{\lim }}\,f\left( x \right)=b-0:\forall \varepsilon >0\ \exists \delta >0:\forall x\in D\left[ f \right]:\left| x \right|>\delta \Rightarrow b-\varepsilon <f\left( x \right)\le b$

Приведем соответствующий пример функции, для которой имеет место равенство 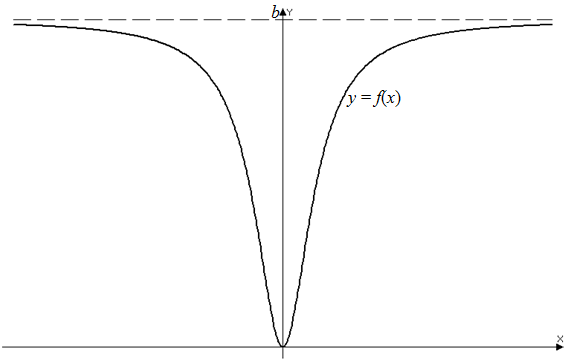$\underset{x\to \infty }{\mathop{\lim }}\,f\left( x \right)=b-0$ (рис. 2).

Рис. 2

Понравился сайт? Расскажи друзьям!