Предел функции на бесконечности
Определение предела функции на бесконечности
![]()
Геометрическое толкование предела функции на бесконечности изображено на рисунке 1.
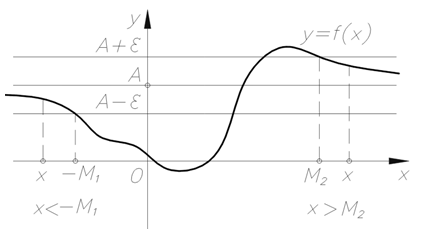
Рис. 1
Число ![]() называется пределом функции
называется пределом функции ![]() при
при ![]() , если для любого числа
, если для любого числа ![]() существует число
существует число ![]() такое, что для всех значений аргумента, больших этого числа, значения функции отличаются по величине от указанного числа
такое, что для всех значений аргумента, больших этого числа, значения функции отличаются по величине от указанного числа ![]() меньше, чем на
меньше, чем на ![]() :
:
![]()
Геометрический смысл предела функции на бесконечности
Геометрический смысл предела функции при ![]() . Преобразуем неравенство
. Преобразуем неравенство ![]() в определении предела функции на плюс бесконечности следующим образом:
в определении предела функции на плюс бесконечности следующим образом:
![]()
или
![]()
Полученное неравенство означает, что график рассматриваемой функции ![]() для всех
для всех ![]() будет лежать в полосе, которая ограничена прямыми
будет лежать в полосе, которая ограничена прямыми ![]() (рис. 2).
(рис. 2).
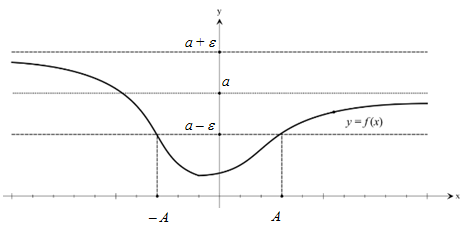
Рис. 2
Число ![]() называется пределом функции
называется пределом функции ![]() при
при ![]() , если для любого числа
, если для любого числа ![]() существует число
существует число ![]() такое, что для всех значений аргумента, меньших этого числа, значения функции отличаются по величине от указанного числа
такое, что для всех значений аргумента, меньших этого числа, значения функции отличаются по величине от указанного числа ![]() меньше, чем на
меньше, чем на ![]() :
:
![]()
Примеры решения задач
| Задание | Используя определение предела функции, доказать равенство |
| Доказательство | То есть необходимо показать, что для любого числа тогда в качестве Итак, Что и требовалось доказать. |
| Задание | Доказать по определению, что |
| Доказательство | Необходимо показать, что для любого числа Рассмотрим верное неравенство то есть получили, что Итак, Что и требовалось доказать. |











