Правило Лопиталя для вычисления пределов

ОПРЕДЕЛЕНИЕ

Теорема (правило) Лопиталя – метод нахождения пределов функций, который позволяет раскрывать неопределенности вида $\left[ \frac{0}{0} \right]$ и $\left[ \frac{\infty }{\infty } \right]$ .

Способ раскрытия такого рода неопределённостей был опубликован в учебнике «Analyse des Inﬁniment Petits» в 1696 году французским математиком, автором первого учебника по математическому анализу, маркизом Гийомом Франсуа Лопиталем (1661-1704). Хотя сам метод был сообщен Лопиталю в письме его первооткрывателем швейцарским математиком, механиком, врачом и филологом-классицистом Иоганном Бернулли (1667-1748).

ПРАВИЛО ЛОПИТАЛЯ

Если

1) $\underset{x\to a}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to a}{\mathop{\lim }}\,g\left( x \right)=0$ или $\underset{x\to a}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to a}{\mathop{\lim }}\,g\left( x \right)=\infty$ ;

2) функции $f\left( x \right)$ и $\quad g\left( x \right)$ дифференцируемы в окрестности точки $x=a$ ;

3) в окрестности этой точки ${g}'\left( x \right)\ne 0$ ;

4) существует $\underset{x\to a}{\mathop{\lim }}\,\frac{{f}'\left( x \right)}{{g}'\left( x \right)}$ ,

то существует и $\underset{x\to a}{\mathop{\lim }}\,\frac{f\left( x \right)}{g\left( x \right)}$ , причем $\underset{x\to a}{\mathop{\lim }}\,\frac{f\left( x \right)}{g\left( x \right)}=\underset{x\to a}{\mathop{\lim }}\,\frac{{f}'\left( x \right)}{{g}'\left( x \right)}$

Замечание 1. Рассматриваемые пределы также могут быть односторонними.

Замечание 2. Правило Лопиталя можно также применять к неопределенностям типа $\left[ 0\cdot \infty \right],\ \left[ \infty -\infty \right],\ \left[ {{0}^{0}} \right],\ \left[ {{1}^{\infty }} \right],\ \left[ {{\infty }^{0}} \right]$ . Первые две неопределенности можно свести к указанным в правиле Лопиталя типам с помощью алгебраических преобразований. А неопределенности последние три сводятся к неопределенности типа $\left[ 0\cdot \infty \right]$ с помощью основного логарифмического тождества $f{{\left( x \right)}^{g\left( x \right)}}={{e}^{\ln f{{\left( x \right)}^{g\left( x \right)}}}}$ .

Примеры решения задач

ПРИМЕР 1

Задание

С помощью правила Лопиталя вычислить предел

$\underset{x\to 0}{\mathop{\lim }}\,\frac{{{a}^{x}}-1}{x}$

Решение

Начнем с выяснения типа неопределенности (если таковая имеется), для этого вместо $x$ в выражение, стоящее под знаком предела, подставляем нуль:

$\frac{{{a}^{0}}-1}{0}=\frac{0}{0}$

Итак, необходимо раскрыть неопределенность вида $\left[ \frac{0}{0} \right]$ . Для этого применим правило Лопиталя:

$\underset{x\to 0}{\mathop{\lim }}\,\frac{{{a}^{x}}-1}{x}\ \left[ \frac{0}{0} \right]\overset{}{\mathop{=}}\,\underset{x\to 0}{\mathop{\lim }}\,\frac{{{\left( {{a}^{x}}-1 \right)}^{\prime }}}{{{\left( x \right)}^{\prime }}}\underset{x\to 0}{\mathop{=\lim }}\,\frac{{{a}^{x}}\ln a-0}{1}\underset{x\to 0}{\mathop{=\lim }}\,{{a}^{x}}\ln a={{a}^{0}}\cdot \ln a=\ln a$

Ответ

ПРИМЕР 2

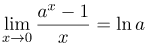Задание

Найти значение предела

$\underset{x\to 2}{\mathop{\lim }}\,\left( \frac{4}{{{x}^{2}}-4}-\frac{1}{x-2} \right)$

Решение

Данный предел содержит неопределенность типа

$\left[ \frac{4}{{{2}^{2}}-4}-\frac{1}{2-2} \right]=\left[ \frac{4}{0}-\frac{1}{0} \right]=\left[ \infty -\infty \right]$

С помощью алгебраических преобразований приведем ее к одной из неопределенностей $\left[ \frac{0}{0} \right]$ или $\left[ \frac{\infty }{\infty } \right]$ . Приведем выражение, предел которого необходимо найти, к общему знаменателю:

$\underset{x\to 2}{\mathop{\lim }}\,\left( \frac{4}{{{x}^{2}}-4}-\frac{1}{x-2} \right)\ \left[ \infty -\infty \right]=\underset{x\to 2}{\mathop{\lim }}\,\frac{4-\left( x+2 \right)}{{{x}^{2}}-4}=\underset{x\to 2}{\mathop{\lim }}\,\frac{2-x}{{{x}^{2}}-4}$

Полученный в результате предел уже имеет неопределенность

$\left[ \frac{2-2}{{{2}^{2}}-4} \right]=\left[ \frac{0}{0} \right]$

поэтому к нему можно применить правило Лопиталя:

$\underset{x\to 2}{\mathop{\lim }}\,\left( \frac{4}{{{x}^{2}}-4}-\frac{1}{x-2} \right)\ \left[ \infty -\infty \right]=\underset{x\to 2}{\mathop{\lim }}\,\frac{2-x}{{{x}^{2}}-4}\ \left[ \frac{0}{0} \right]\overset{}{\mathop{=}}\,\underset{x\to 2}{\mathop{\lim }}\,\frac{{{\left( 2-x \right)}^{\prime }}}{{{\left( {{x}^{2}}-4 \right)}^{\prime }}}=$

$=\underset{x\to 2}{\mathop{\lim }}\,\frac{0-1}{2x-0}=\underset{x\to 2}{\mathop{\lim }}\,\frac{-1}{2x}=-\frac{1}{2\cdot 2}=-\frac{1}{4}$

Ответ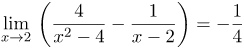