Односторонние пределы

ОПРЕДЕЛЕНИЕ

Под односторонним пределом числовой функции подразумевают «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) (рис. 1) и правосторонним пределом (пределом справа) (рис. 2).

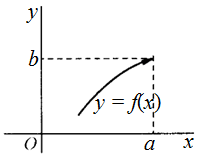
Рис. 1

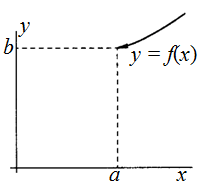
Рис. 2

Определение одностороннего предела функции по Гейне

ОПРЕДЕЛЕНИЕ

Число $b\in R$ называется правосторонним пределом (или правым пределом, или пределом справа) некоторой функции $f\left( x \right)$ в точке $x=a$ , если для всякой последовательности $\left\{ {{x}_{n}} \right\},\ {{x}_{n}}>a$ , которая сама сходится к числу $a$ , соответствующая последовательность значений функции $\left\{ f\left( {{x}_{n}} \right) \right\}$ сходится к $b$ .

Обозначение:

$\underset{x\to a+0}{\mathop{\lim }}\,f\left( x \right),\ \underset{x\to a+}{\mathop{\lim }}\,f\left( x \right),\ \underset{x\downarrow a}{\mathop{\lim }}\,f\left( x \right),\ f\left( a+0 \right),\ f\left( a+ \right)$

Итак,

$\underset{x\to a+0}{\mathop{\lim }}\,f\left( x \right)=b\Leftrightarrow \forall \left\{ {{x}_{n}} \right\}:\left( {{x}_{n}}>a\ \forall \,n\in N \right)\wedge \underset{n\to \infty }{\mathop{\lim }}\,{{x}_{n}}=a\Rightarrow \underset{n\to \infty }{\mathop{\lim }}\,f\left( {{x}_{n}} \right)=b$

ОПРЕДЕЛЕНИЕ

Число $b\in R$ называется левосторонним пределом (или левым пределом, или пределом слева) функции $f\left( x \right)$ в точке $a$ , если для всякой последовательности $\left\{ {{x}_{n}} \right\}\ \left( {{x}_{n}}<a \right)$ , сходящейся к $a$ , соответствующая последовательность значений функции $\left\{ f\left( {{x}_{n}} \right) \right\}$ сходится к числу $b$ .

Обозначение:

$\underset{x\to a-0}{\mathop{\lim }}\,f\left( x \right),\ \underset{x\to a-}{\mathop{\lim }}\,f\left( x \right),\ \underset{x\uparrow a}{\mathop{\lim }}\,f\left( x \right),\ f\left( a-0 \right),\ f\left( a- \right)$

То есть

$\underset{x\to a+0}{\mathop{\lim }}\,f\left( x \right)=b\Leftrightarrow \forall \left\{ {{x}_{n}} \right\}:\left( {{x}_{n}}<a\ \forall \,n\in N \right)\wedge \underset{n\to \infty }{\mathop{\lim }}\,{{x}_{n}}=a\Rightarrow \underset{n\to \infty }{\mathop{\lim }}\,f\left( {{x}_{n}} \right)=b$

Определение одностороннего предела по Коши

ОПРЕДЕЛЕНИЕ

Число $b\in R$ называется правосторонним пределом (правым пределом, пределом справа) некоторой функции $f\left( x \right)$ в точке $a$ , если для любого числа $\varepsilon >0$ существует такое положительное число $\delta =\delta \left( \varepsilon \right)$ , что для всех точек $x\in \left( a;\ a+\delta \right)$ справедливо неравенство $\left| f\left( x \right)-b \right|<\varepsilon$ :

$\underset{x\to a+0}{\mathop{\lim }}\,f\left( x \right)=b\Leftrightarrow \forall \varepsilon >0\ \exists \delta =\delta \left( \varepsilon \right)>0:\forall x\in \left( a;\ a+\delta \right):\left| f\left( x \right)-b \right|<\varepsilon$

ОПРЕДЕЛЕНИЕ

Число $b\in R$ называется левосторонним пределом (левым пределом, пределом слева) функции $f\left( x \right)$ в точке $a$ , если для всякого положительного числа $\varepsilon$ существует такое положительное число $\delta =\delta \left( \varepsilon \right)$ , что для всех точек $x\in \left( a-\delta ;\ a \right)$ справедливо неравенство $\left| f\left( x \right)-b \right|<\varepsilon$ :

$\underset{x\to a+0}{\mathop{\lim }}\,f\left( x \right)=b\Leftrightarrow \forall \varepsilon >0\ \exists \delta =\delta \left( \varepsilon \right)>0:\forall x\in \left( a-\delta ;\ a \right):\left| f\left( x \right)-b \right|<\varepsilon$

Замечание. Основные свойства односторонних пределов схожи со свойствами обычных пределов.

ТЕОРЕМА

Для существования (двустороннего) предела функции необходимо и достаточно, чтобы оба односторонних предела существовали и равнялись между собой.

Примеры решения задач

ПРИМЕР 1

Задание

Найти односторонние пределы в точке $x=0$ у кусочно-непрерывной функции

$f(x)=\left\{ \begin{matrix} & x^{2},\ x\le 0; \\ & x-1,\ x>0 \\ \end{matrix} \right.$

Решение

Найдем правый предел $\underset{x\to 0+0}{\mathop{\lim }}\,f\left( x \right)$ заданной функции. Если $x$ стремится к нулю справа, то он остается большим, чем это значение. А для $x>0$ функция $f\left( x \right)$ задается следующим аналитическим выражением:

$f\left( x \right)=x-1,\ x>0$

То есть

$f\left( 0+0 \right)=\underset{x\to 0+0}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to 0+0}{\mathop{\lim }}\,\left( x-1 \right)=0+0-1=-1$

Аналогично левый предел

$f\left( 0-0 \right)=\underset{x\to 0-0}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to 0-0}{\mathop{\lim }}\,{{x}^{2}}={{\left( 0-0 \right)}^{2}}=0$

Ответ

$f\left( 0+0 \right)=-1, \quad f\left( 0-0 \right)=0$

ПРИМЕР 2

Задание

Исследовать на непрерывность в точке $x=1$ функцию

$f\left( x \right)=\frac{{{x}^{2}}-1}{x-1}$

Решение

Известно, что функция будет непрерывной в некоторой точке, если ее правый предел в этой точке равен левому пределу и равен значению функции в исследуемой точке. Иначе, в указанной точке функция терпит разрыв.

Таким образом, нам необходимо найти односторонние пределы и значение заданной функции в точке $x=1$ . Правый предел

$f\left( 1+0 \right)=\underset{x\to 1+0}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to 1+0}{\mathop{\lim }}\,\frac{{{x}^{2}}-1}{x-1}=\underset{x\to 1+0}{\mathop{\lim }}\,\frac{\left( x-1 \right)\left( x+1 \right)}{x-1}=$

$=\underset{x\to 1+0}{\mathop{\lim }}\,\left( x+1 \right)=1+0+1=2$

Аналогично левый предел

$f\left( 1-0 \right)=\underset{x\to 1-0}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to 1-0}{\mathop{\lim }}\,\frac{{{x}^{2}}-1}{x-1}=\underset{x\to 1-0}{\mathop{\lim }}\,\frac{\left( x-1 \right)\left( x+1 \right)}{x-1}=$

$=\underset{x\to 1-0}{\mathop{\lim }}\,\left( x+1 \right)=1-0+1=2$

В точке $x=1$ функция $f\left( x \right)$ неопределенна.

Итак, так как $f\left( 1+0 \right)=f\left( 1-0 \right)$ , но в точке $x=1$ значение функции не существует, то точка $x=1$ является точкой устранимого разрыва.

Ответ

Точка $x=1$ – точка устранимого разрыва.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Односторонние пределы

Определение одностороннего предела функции по Гейне

Определение одностороннего предела по Коши

Примеры решения задач