Формулы пределов функций
При вычислении пределов зачастую используют понятия непрерывности функции в точке, предела функции на бесконечности, а также свойства пределов непрерывной функции.
Замечание. Таким образом, для элементарных функций, предел в любой точке из их области определения, кроме граничных, можно вычислять как значение соответствующей функции в этих точках.
| Задание | Вычислить предел |
| Решение | Так как функция |
| Ответ |
Замечание. В граничных точках области определения вычисляются односторонние пределы.
Свойства пределов функций
1. Константу можно выносить за знак предела:
![]()
Пример.
![]()
2. Предел произведения функций равен произведению пределов от каждого из сомножителей при условии, что последние пределы существуют:
![]()
Пример.
![]()
3. Для непрерывных функций знак предельного перехода и знак функции можно менять местами:
![]()
Пример.
![]()
Таблица пределов функций
1. Предел константы равен этой константе:
![]()
где ![]() – некоторое действительное число, конечное или бесконечное.
– некоторое действительное число, конечное или бесконечное.
2. Предел коренной функции ![]() :
:
![]() , для любого натурального n
, для любого натурального n
![]()
![]()
3. Предел степенной функции ![]() :
:
![]()
![]()
![]()
![]()
![]()
4. Предел показательной функции ![]() :
:
![]()
![]()
5. Предел логарифмической функции ![]() :
:
![]()
![]()
![]()
6. Предел тригонометрических функций:
![]() не существуют;
не существуют;
![]()
![]()
![]()
7. Предел обратных тригонометрических функций:
![]()
![]()
![]()
![]()
Примеры решения задач
| Задание | Вычислить предел
|
| Решение | Данный предел неопределенности не имеет, так как и числитель и знаменатель функции, стоящей под знаком предела, при |
| Ответ | 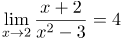 |
| Задание | Вычислить предел |
| Решение | Согласно таблице пределов (а именно предел показательной функции)
при |
| Ответ |











