Газовые законы
Газовые законы были открыты экспериментально, но все они могут быть получены из уравнения Менделеева-Клапейрона.
Рассмотрим каждый из них.
Закон Бойля-Мариотта (изотермический процесс)
Изотермическим процессомназывают изменение состояния газа, при котором его температура остаётся постоянной.
Для неизменной массы газа при постоянной температуре произведение давления газа на объем есть величина постоянная:
![]()
Этот же закон можно переписать в другом виде (для двух состояний идеального газа):
![]()
Этот закон следует из уравнения Менделеева – Клапейрона:
![]()
Очевидно, что при неизменной массе газа и при постоянной температуре правая часть уравнения остается постоянной величиной.
Графики зависимости параметров газа при постоянной температуре называются изотермами.
Обозначив константу буквой ![]() , запишем функциональную зависимость давления от объема при изотермическом процессе:
, запишем функциональную зависимость давления от объема при изотермическом процессе:
![]()
Видно, что давление газа обратно пропорционально его объему. Графиком обратной пропорциональности, а, следовательно, и графиком изотермы в координатах ![]() является гипербола (рис.1, а). На рис.1 б) и в) представлены изотермы в координатах
является гипербола (рис.1, а). На рис.1 б) и в) представлены изотермы в координатах ![]() и
и ![]() соответственно.
соответственно.
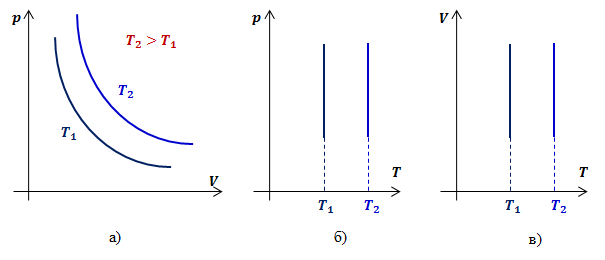
Рис.1. Графики изотермических процессов в различных координатах
Закон Гей-Люссака (изобарный процесс)
Изобарным процессомназывают изменение состояния газа, при котором его давление остаётся постоянным.
Для неизменной массы газа при постоянном давлении отношение объема газа к температуре есть величина постоянная:
![]()
Для двух состояний газа этот закон запишется в виде:
![]()
Этот закон также следует из уравнения Менделеева – Клапейрона:
![]()
Графики зависимости параметров газа при постоянном давлении называются изобарами.
Рассмотрим два изобарных процесса с давлениями![]() и
и ![]() . В координатах
. В координатах ![]() и
и ![]() изобары будут иметь вид прямых линий, перпендикулярных оси
изобары будут иметь вид прямых линий, перпендикулярных оси ![]() (рис.2 а,б).
(рис.2 а,б).
Определим вид графика в координатах ![]() .Обозначив константу буквой
.Обозначив константу буквой ![]() , запишем функциональную зависимость объема от температуры при изобарном процессе:
, запишем функциональную зависимость объема от температуры при изобарном процессе:
![]()
Видно, что при постоянном давлении объем газа прямо пропорционален его температуре. Графиком прямой пропорциональности, а, следовательно, и графиком изобары в координатах ![]() является прямая, проходящая через начало координат (рис.2, в). В реальности при достаточно низких температурах все газы превращаются в жидкости, к которым газовые законы уже неприменимы. Поэтому вблизи начала координат изобары на рис.2, в) показаны пунктиром.
является прямая, проходящая через начало координат (рис.2, в). В реальности при достаточно низких температурах все газы превращаются в жидкости, к которым газовые законы уже неприменимы. Поэтому вблизи начала координат изобары на рис.2, в) показаны пунктиром.
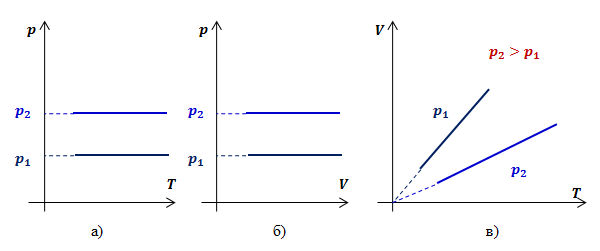
Рис.2. Графики изобарных процессов в различных координатах
Закон Шарля (изохорный процесс)
Изохорным процессомназывают изменение состояния газа, при котором его объем остаётся постоянным.
Для неизменной массы газа при постоянном объеме отношение давления газа к его температуре есть величина постоянная:
![]()
Для двух состояний газа этот закон запишется в виде:
![]()
Этот закон также можно получить из уравнения Менделеева – Клапейрона:
![]()
Графики зависимости параметров газа при постоянном давлении называются изохорами.
Рассмотрим два изохорных процесса с объемами ![]() и
и ![]() . В координатах
. В координатах ![]() и
и ![]() графиками изохор будут прямые, перпендикулярные оси
графиками изохор будут прямые, перпендикулярные оси ![]() (рис.3 а, б).
(рис.3 а, б).
Для определения вида графика изохорного процесса в координатах ![]() обозначим константу в законе Шарля буквой
обозначим константу в законе Шарля буквой ![]() , получим:
, получим:
![]()
Таким образом, функциональная зависимость давления от температуры при постоянном объеме является прямой пропорциональностью, графиком такой зависимости является прямая, проходящая через начало координат (рис.3, в).
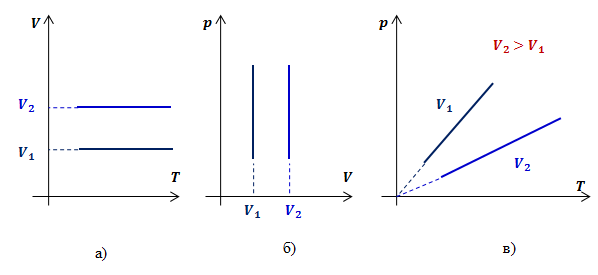
Рис.3. Графики изохорных процессов в различных координатах
Примеры решения задач
| Задание | До какой температуры нужно изобарически охладить некоторую массу газа с начальной температурой |
| Решение | Изобарный процесс По условию задачи объем газа вследствие изобарного охлаждения уменьшается на одну четверть, следовательно: Тогда: откуда конечная температура газа: Переведем единицы в систему СИ: начальная температура газа Вычислим: |
| Ответ | Газ нужно охладить до температуры |
| Задание | В закрытом сосуде находится газ под давлением 200 кПа. Каким станет давление газа, если температуру повысить на 30%? |
| Решение | Так как сосуд с газом закрытый, объем газа не меняется. Изохорный процесс описывается законом Шарля:
По условию задачи температура газа повысилась на 30%, поэтому можно записать: Подставив последнее соотношение в закон Шарля, получим: откуда Переведем единицы в систему СИ: начальное давление газа Вычислим: |
| Ответ | Давление газа станет равным 260 кПа. |
| Задание | В кислородной системе, которой оборудован самолет, имеется |
| Решение | Изотермический процесс откуда давление, установившееся в системе: Вычислим: |
| Ответ | В системе установится давление |
| Задание | На рисунке дан график изменения состояния идеального газа в координатах 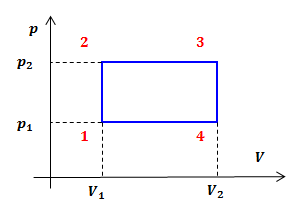
|
| Ответ | Переходы В координатах 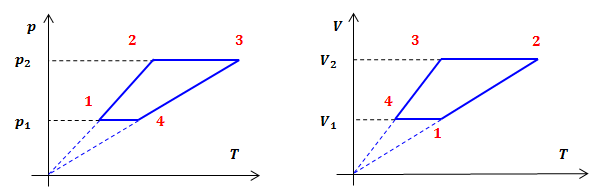
|











