Эффект Доплера
Формула и определение эффекта Доплера
Эффект Доплера описывается формулой:
![]()
где ![]() — частота волны, регистрируемой приемником;
— частота волны, регистрируемой приемником; ![]() — частота волны, испускаемой источником;
— частота волны, испускаемой источником; ![]() —скорость звука в среде;
—скорость звука в среде; ![]() и
и ![]() — скорости приемника и источника относительно упругой среды соответственно.
— скорости приемника и источника относительно упругой среды соответственно.
Если источник звука приближается к приемнику, то его скорость имеет знак «плюс». Если источник удаляется от приемника, его скорость имеет знак «минус».
Из формулы видно, что при таком движении источника и приемника, при котором расстояние между ними уменьшается, воспринимаемая приемником частота ![]() оказывается больше частоты источника
оказывается больше частоты источника ![]() . Если расстояние между источником и приемником увеличивается,
. Если расстояние между источником и приемником увеличивается, ![]() будет меньше, чем
будет меньше, чем ![]() .
.
Эффект Доплера лежит в основе радаров, с помощью которых сотрудники ГАИ определяют скорость автомобиля. В медицине используют эффект Доплера для того, чтобы с помощью ультразвукового прибора отличить вены от артерий при проведении инъекций. Благодаря эффекту Доплера, астрономы установили, что Вселенная расширяется — галактики разбегаются друг от друга. С помощью эффекта Доплера определяются параметры движения планет и космических аппаратов.
Примеры решения задач
| Задание | На шоссе сближаются два автомобиля со скоростями |
| Решение | Запишем формулу для эффекта Доплера:
До встречи автомобили сближаются т.е. расстояние между ними уменьшается и источник звука (первый автомобиль) приближается к приемнику звука (второму автомобилю), поэтому скорость первого автомобиля войдет в формулу со знаком «плюс». Вычислим:
После встречи автомобили будут удаляться друг от друга, т.е. источник звукового сигнала будет удаляться от приемника, поэтому скорость источника войдет в формулу со знаком «минус»:
|
| Ответ | Частота сигнала, который услышит водитель второй автомашины до встречи с первой, составит 732 Гц, а после встречи – 616 Гц. |
| Задание | Скорый поезд приближается к стоящему на путях электропоезду со скоростью 72 км/ч. Электропоезд подает звуковой сигнал частотой 0,6 кГц. Определить кажущуюся частоту звукового сигнала, который услышит машинист скорого поезда. Скорость звука принять равной 340 м/с. |
| Решение | Запишем формулу для эффекта Доплера:
В системе отсчета, связанной со скорым поездом, машинист скорого поезда (приемник сигнала) неподвижен, поэтому Переведем единицы в систему СИ: скорость движения электропоезда относительно скорого поезда Вычислим:
|
| Ответ | Кажущаяся частота звукового сигнала, который услышит машинист скорого поезда, 638 Гц. |
| Задание | Мимо железнодорожной платформы проходит электропоезд. Наблюдатель, стоящий на платформе, слышит звук сирены поезда. Когда поезд приближается? наблюдатель слышит звук частотой 1100 Гц, когда поезд удаляется, кажущаяся частота звука 900 Гц. Найти скорость электровоза и частоту звука, издаваемого сиреной. Скорость звука в воздухе принять равной 340 м/с. |
| Решение | Так как наблюдатель, стоящий на платформе, неподвижен, скорость приемника Запишем формулу для эффекта Доплера для обоих случаев. а) когда поезд приближается: б) когда поезд удаляется: Выразим частоты звукового сигнала сирены или откуда находим скорость электровоза: Вычислим: Частота звука, издаваемого сиреной: Вычислим:
|
| Ответ | Скорость электровоза 34 м/с; частота звука, издаваемого сиреной, 990 Гц. |






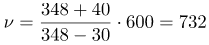 Гц
Гц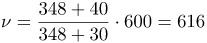 Гц
Гц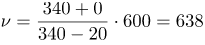 Гц
Гц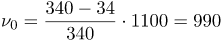 Гц
Гц




