Равномерное прямолинейное движение
В этом случае траекторией движения является прямая. Скорость тела остается постоянной как по модулю, так и по направлению: ![]() .
.
Закон движения в случае равномерного прямолинейного движения имеет вид:
![]()
где ![]() — радиус-вектор точки в момент времени
— радиус-вектор точки в момент времени ![]() ,
, ![]() — радиус-вектор начального положения точки,
— радиус-вектор начального положения точки, ![]() — скорость.
— скорость.
В одномерном случае закон движения запишется в виде:
![]()
В случае движения на плоскости закон движения запишется в виде системы двух уравнений:
![Rendered by QuickLaTeX.com \[ \begin{cases} x=x_{0}+v_{x}t \\ y=y_{0}+v_{y}t \end{cases} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-074c640289ff248de74938ce07f0c321_l3.png)
Так как при равномерном прямолинейном движении направление скорости не меняется, то в этом случае путь всегда равен модулю перемещения:
![]()
Изобразим графически зависимость кинематических величин от времени (рис.1).
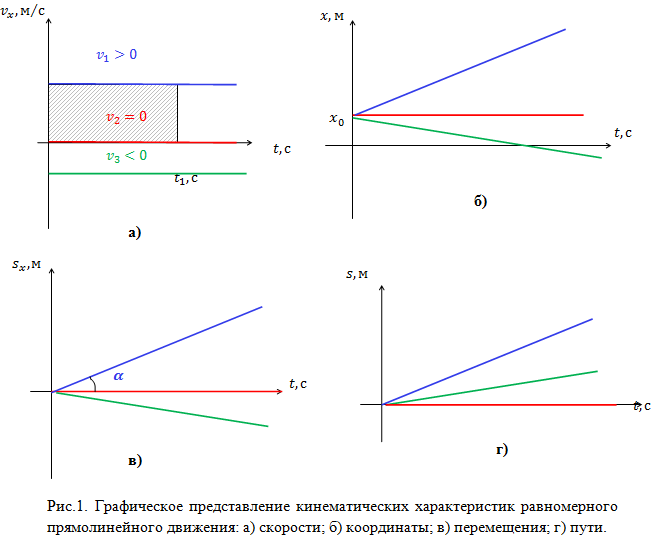
На рис.1 (а) представлены графики зависимости скоростей трех тел от времени. Тело 1 движется со скоростью ![]() в направлении оси
в направлении оси ![]() , тело 2 находится в состоянии покоя, тело 3 движется со скоростью
, тело 2 находится в состоянии покоя, тело 3 движется со скоростью ![]() в направлении, противоположном оси
в направлении, противоположном оси ![]() . Площадь заштрихованного прямоугольника численно равна пути (модулю перемещения), пройденному телом 1 за некоторое время
. Площадь заштрихованного прямоугольника численно равна пути (модулю перемещения), пройденному телом 1 за некоторое время ![]() .
.
Графики движения (зависимости координат тела от времени) изображены на рис.1 (б). На рис.1 (в) представлены графики зависимости перемещений этих тел от времени. По наклону графика перемещения к оси времени можно определить скорость движения тела:
![]()
Графики пройденного пути для каждого из трех тел изображены на рис. 1 (г).
Для нахождения уравнения траектории нужно исключить время из уравнений и получить зависимость ![]() .
.
Примеры решения задач по теме «Равномерное прямолинейное движение»
| Задание | От заправочной станции отправился автобус со скоростью 54 км/ч. Через 5 мин вслед за ним выехал легковой автомобиль со скоростью 72 км/ч. Через какое время и на каком расстоянии от заправочной станции автомобиль догонит автобус? |
| Решение | 1) Аналитический способ.
Совмести начало координат с положением заправочной станции и направим ось Автомобиль и автобус совершают равномерное прямолинейное движение, закон движения в этом случае имеет вид: Так как и автобус, и автомобиль отправились от заправочной станции, начальные координаты для них равны нулю Уравнение движения автобуса: Автомобиль выехал на В момент, когда автомобиль догонит автобус, их координаты будут равны: Из последнего соотношения находим время, через которое автомобиль догонит автобус: Переведем значения физических величин в систему СИ. Время в системе СИ измеряется в секундах, поэтому Вычислим время, через которое автомобиль догонит автобус:
Подставим это значение времени в любое из уравнений движения и вычислим расстояние от заправочной станции. на котором одно транспортное средство догонит другое:
2) Графический способ. Запишем законы движения для автобуса и автомобиля: и построим графики в одной системе координат. 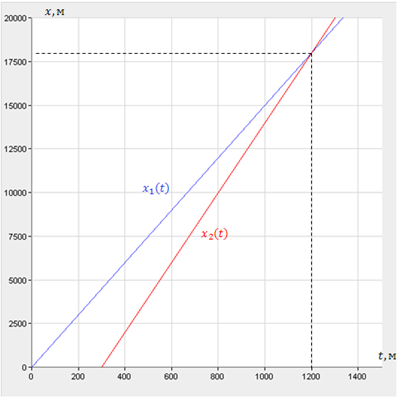
Координаты точки пересечения графиков дадут нам значения времени, когда автомобиль догонит автобус и расстояния от заправочной станции, на котором это произойдет. По графику видно, что |
| Ответ | Автомобиль догонит автобус через 20 минут и на расстоянии 18 км от заправочной станции. |
| Задание | Движение материальной точки в данной системе отсчета описывается уравнениями |
| Решение | Выразим время из второго уравнения:
и подставим это выражение в первое уравнение: Последнее выражение и есть уравнение траектории. Определим положение точки 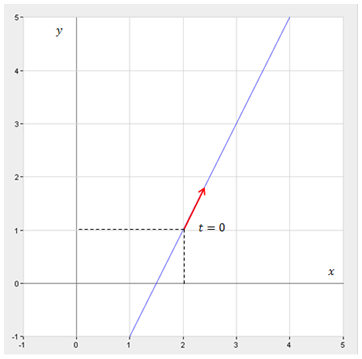
Из уравнений движения определим компоненты вектора скорости: компоненты вектора скорости равны числовым коэффициентам при переменной
Скорость движения:
|
| Ответ | Уравнение траектории материальной точки |






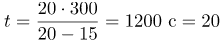 (минут)
(минут)




