Закон Паскаля. Гидростатическое давление

Закон Паскаля для жидкости

ОПРЕДЕЛЕНИЕ

Закон Паскаля — давление на поверхность жидкости, произведенное внешними силами, передается жидкостью одинаково во всех направлениях.

Этот закон был открыт французским ученым Б. Паскалем в 1653 г. Его иногда называют основным законом гидростатики.

Закон Паскаля можно объяснить с точки зрения молекулярного строения вещества. В твердых телах молекулы образуют кристаллическую решетку и колеблются около своих положений равновесия. В жидкостях и газах молекулы обладают относительной свободой, они могут перемещаться друг относительно друга. Именно эта особенность позволяет давление, производимое на жидкость (или газ) передавать не только в направлении действия силы, но и во всех направлениях.

Закон Паскаля нашел широкое применение в современной технике. На законе Паскаля основана работа современных суперпрессов, которые позволяют создавать давления порядка 800 МПа. Также на этом законе построена работа всей гидроавтоматики, управляющей космическими кораблями, реактивными авиалайнерами, станками с числовым программным управлением, экскаваторами, самосвалами и т.д.

Гидростатическое давление жидкости

ОПРЕДЕЛЕНИЕ

Гидростатическое давление — это давление в жидкости, обусловленное силой тяжести.

Гидростатическое давление внутри жидкости на любой глубине не зависит от формы сосуда, в котором находится жидкость, и равно произведению плотности жидкости, ускорения свободного падения и глубины, на которой определяется давление:

$p=\rho gh$

В однородной покоящейся жидкости давления в точках, лежащих в одной горизонтальной плоскости (на одном уровне), одинаковы. Во всех случаях, приведенных на рис. 1, давление жидкости на дно сосудов одинаково.

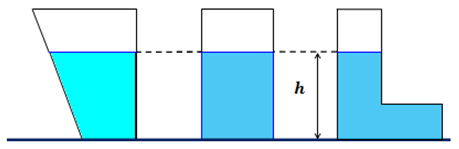
Рис.1. Независимость гидростатического давления от формы сосуда

На данной глубине жидкость давит одинаково по всем направлениям, поэтому давление на стенку на данной глубине будет таким же, как и на горизонтальную площадку, расположенную на такой же глубине.

Полное давление в жидкости, налитой в сосуд, складывается из давления у поверхности жидкости и гидростатического давления:

$p=p_0+\rho gh$

Давление у поверхности жидкости часто равно атмосферному давлению.

Примеры решения задач

ПРИМЕР 1

Задание

В полый куб с ребром 40 см налита вода. Найти силу давления воды на дно и стенки куба.

Решение

Выполним рисунок.

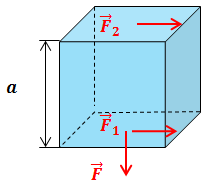
1) Гидростатическое давление на глубине $a:$

$p=\rho ga$

Сила давления воды на дно куба:

$F=pS$

где $S$ — площадь дна; $S=a^2$ ,

поэтому:

$F=\rho ga\cdot a^2=\rho ga^3$

2) Среднее давление на боковую грань равно полусумме давлений на уровне поверхности и на уровне дна:

$p=\frac{p_1+p_2}{2}=\frac{\rho ga}{2}\$

сила давления на стенку куба:

$F=\frac{\rho ga}{2}\cdot a^2=\frac{\rho ga^3}{2}$

Из таблиц плотность воды $\rho =1000$ кг/м $^{3}$ .

Ускорение свободного падения $g=9,8$ м/с $^{2}$ .

Переведем единицы в систему СИ: длина ребра куба $a=40$ см $=0,4$ м.

Вычислим:

1) сила давления на дно:

$F=1000\cdot 9,8\cdot {0,4}^3=627\ H;$

2) сила давления на стенку:

$F=\frac{1000\cdot 9,8\cdot {0,4}^3}{2}=314\ H$

Ответ

Силы давления воды на дно и стенки куба 627 и 314 Н соответственно.

ПРИМЕР 2

Задание

В два колена U-образной трубки налиты вода и масло, разделенные ртутью. Поверхности раздела ртути и жидкостей в обоих коленах находятся на одной высоте. Определить высоту столба воды, если высота столба масла 20 см.

Решение

Выполним рисунок.