Логарифмы
Определение и основные понятия логарифмов
Логарифмом числа ![]() по основанию
по основанию ![]() называется такое число
называется такое число ![]() , при котором имеет место равенство
, при котором имеет место равенство ![]() :
:
![]() , причем
, причем ![]() .
.
Число ![]() называется основанием логарифма, а
называется основанием логарифма, а ![]() — подлогарифмической функцией.
— подлогарифмической функцией.
Например. ![]() , поскольку
, поскольку ![]() .
.
В 8 веке индийский математик Вирасена (792-853), исследуя степенные зависимости, опубликовал фактически таблицу логарифмов (целочисленных показателей) для оснований 2, 3, 4. Дальнейшее развитие теория логарифмов получила в средневековой Европе, где была выдвинута идея замены трудоемкого умножения на простое сложение. Впервые эта идея увидела свет в книге «Arithmetica integra» (1544) немецкого математика Михаэля Штифеля (1487-1567). В 1614 году шотландский математик Джон Непер (1560-1617) опубликовал сочинение «Описание удивительной таблицы логарифмов», в котором ввел термин «логарифм», а также описал его свойства. Общепринятого обозначения логарифма не было до конца 19 века, хотя специальные обозначения для натурального и десятичного логарифмов появились значительно ранее.
Натуральный логарифм ![]() — логарифм по основанию
— логарифм по основанию ![]() :
:
![]()
Десятичный логарифм ![]() — логарифм по основанию 10:
— логарифм по основанию 10:
![]()
Свойства логарифмов
Следующие свойства приведены для произвольных величин ![]() , при которых логарифм существует.
, при которых логарифм существует.
- Основное логарифмическое тождество:
![Rendered by QuickLaTeX.com \[a^{\log _{a} b} =b\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f8be4b7204f42764eebfaf71cee28940_l3.png)
Например.
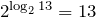 .
. - Если основание логарифма и подлогарифмическая функция равны, то логарифм равен единице:
![Rendered by QuickLaTeX.com \[\log _{a} a=1\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-4f80568327dbe9c3936768a0c7aae4e4_l3.png)
Например.
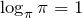 .
. - Логарифм по любому основанию от единицы равен нулю:
![Rendered by QuickLaTeX.com \[\log _{a} 1=0\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-8087747756cddb4d1e2595dd4ee4baea_l3.png)
Например.
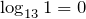 .
. - Логарифм произведения равен сумме логарифмов от каждого из сомножителей:
![Rendered by QuickLaTeX.com \[\log _{a} \left(b\cdot c\right)=\log _{a} b+\log _{a} c\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-de7fd8ccdd62324a21e56a7b0eb5aac6_l3.png)
Например.
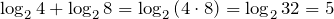 .
. - Логарифм частного равен разности логарифмов от делимого и делителя соответственно:
![Rendered by QuickLaTeX.com \[\log _{a} \frac{b}{c} =\log _{a} b-\log _{a} c\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-35cac62b8522f6762c1f7c47a1c8edd0_l3.png)
Например.
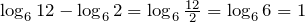 .
. 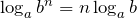 .
.
Например.
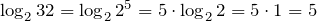 .
.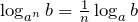 .
.
Например.
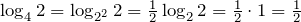 .
.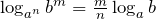 .
.
Например.
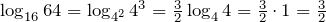 .
.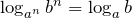 .
.
Например.
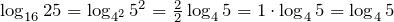 .
.- Переход к новому основанию:
![Rendered by QuickLaTeX.com \[\log _{a} b=\frac{\log _{c} b}{\log _{c} a} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-a3ea8a960690594ab753c3a8eb4851b1_l3.png)
Например.
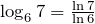 .
. 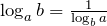 .
.
Например.
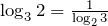 .
.











