Интеграл арктангенса
Интеграл от арктангенса равен переменной интегрирования, умноженной на этот арктангенс, минус логарифм натуральный корня из суммы единицы и переменной интегрирования в квадрате плюс константа интегрирования
![Rendered by QuickLaTeX.com \[ \int{\text{arctg}\,xdx}=x\cdot \text{arctg}\,x-\ln \sqrt{1+{{x}^{2}}}+C \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-cf312c844454c8331ad138176fa86b70_l3.png)
Примеры решения задач
| Задание | Доказать, что |
| Решение | Для доказательства указанной формулы применим метод интегрирования частями:
Что и требовалось доказать. |
| Задание | Найти интеграл |
| Решение | Для сведения интеграла к известной формуле применим метод замены переменной:
|
| Ответ | 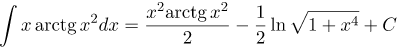 |






![Rendered by QuickLaTeX.com \[\int{\text{arctg}\,x\,dx}\ \left\| \begin{matrix} u=\text{arctg}\,x ,\ dv=dx \\ du=\frac{dx}{1+{{x}^{2}}} ,\ v=x \\ \end{matrix} \right\|=x\cdot \text{arctg}\,x-\int{\frac{xdx}{1+{{x}^{2}}}}\ \left\| \begin{matrix} 1+{{x}^{2}}=t \\ 2xdx=dt \\ xdx=\frac{dt}{2} \\ \end{matrix} \right\|=\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-80b82ae79f93782f9e4f2de597198d0e_l3.png)
![Rendered by QuickLaTeX.com \[\int{x\,\text{arctg}\,{{x}^{2}}dx}\ \left\| \begin{matrix} {{x}^{2}}=t \\ 2xdx=dt \\ xdx=\frac{dt}{2} \\ \end{matrix} \right\|=\int{\text{arctg}\,t\cdot \frac{dt}{2}}=\frac{1}{2}\int{\text{arctg}\,tdt}=\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-85dbfcf329501377fae6d47d7ea04823_l3.png)





