Сумма кубов

ОПРЕДЕЛЕНИЕ

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

$a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})$

Выражение $a^{2}-ab+b^{2}$ , стоящее в правой части равенства, называется неполный квадрат разности. От полного квадрата разности оно отличается лишь отсутствием двойки у второго слагаемого.

Данная формула верна и «справа налево», то есть имеет место соотношение:

$(a+b)(a^{2}-ab+b^{2})=a^{3}+b^{3}$

При помощи этих формул можно раскладывать на множители многочлены.

Примеры решения задач по теме «Сумма кубов»

ПРИМЕР 1

Задание

Разложить на множители двучлен $8u^{3}+v^{3}$ .

Решение

Представим каждое слагаемое в виде:

$8u^{3}+v^{3} = 2^{3} \cdot u^{3} + v^{3} = (2u)^{3} + v^{3} = (2u+v)((2u)^{2} - 2u \cdot v + v^{2}) =$

$= (2u+v)(4u^{2} - 2uv + v^{2})$

Ответ

$8u^{3}+v^{3} = (2u+v)(4u^{2} - 2uv + v^{2})$

ПРИМЕР 2

Задание	Найти произведение многочленов $a^{2}+b$ и $a^{4}-a^{2}b +b^{2}$ .
Решение	Согласно формуле «сумма кубов», имеем: $(a^{2}+b)(a^{4}-a^{2}b +b^{2}) = (a^{2}+b)((a^{2})^{2}-a^{2}b +b^{2}) = (a^{2})^{3} + b^{3} = a^{6}+b^{3}$
Ответ	$(a^{2}+b)(a^{4}-a^{2}b +b^{2}) = a^{6}+b^{3}$

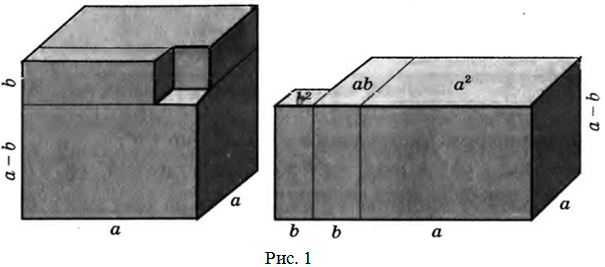
Рассматриваемую формулу «сумма кубов» для положительных величин $a$ и $b$ можно проиллюстрировать геометрически (рис. 1).

Понравился сайт? Расскажи друзьям!