Формулы интеграла
Неопределенный интеграл есть множество всех первообразных, то есть
![]()
где ![]() – некоторая константа.
– некоторая константа.
Найти неопределенный интеграл – это значит найти определенную функцию ![]() пользуясь некоторыми правилами, приемами и таблицей интегралов. Ниже подробно разобраны все правила интегрирования и формулы интеграла.
пользуясь некоторыми правилами, приемами и таблицей интегралов. Ниже подробно разобраны все правила интегрирования и формулы интеграла.
Таблица интегралов
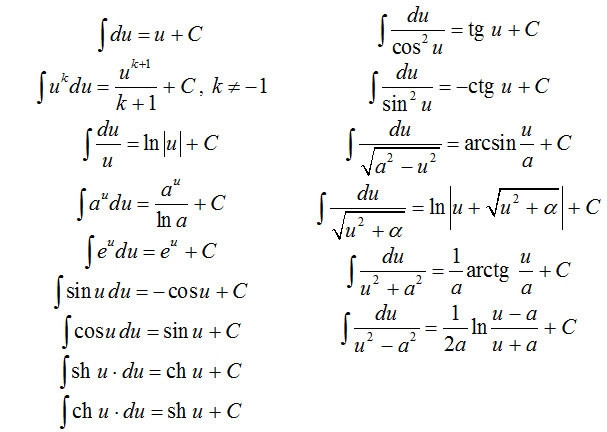
Правила интегрирования
![]()
![]()
![]()
![]()
![]()
Если
![]()
то
![]()
| Задание | Найти интеграл
|
| Решение | Согласно формуле интеграла
при |
| Ответ | 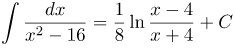 |
| Задание | Найти неопределенный интеграл
|
| Решение | Применим формулу интеграла
При |
| Ответ | 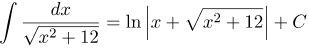 |











