Решение треугольников

Определение и формулы для решения треугольников

ОПРЕДЕЛЕНИЕ

Треугольником называется фигура, состоящая из трех точек и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – сторонами треугольника. Стороны треугольника образуют три угла в треугольнике.

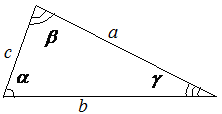
Стороны треугольника обычно обозначают буквами $a,b,c$ , а противолежащие углы – $\alpha ,\beta ,\gamma$ .

Решение треугольников заключается в отыскании всех неизвестных сторон и всех неизвестных углов треугольника по известным данным.

При решении задач используют теорему косинусов или теорему синусов.

Теоремы для решения треугольников

Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

$c^{2} =a^{2} +b^{2} -2ab\cos \gamma ,$

$a^{2} =c^{2} +b^{2} -2cb\cos \alpha ,$

$b^{2} =a^{2} +c^{2} -2ab\cos \beta$

Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной вокруг треугольника окружности:

$\frac{a}{\sin \alpha } =\frac{b}{\sin \beta } =\frac{c}{\sin \gamma } =2R$

Также используют условия, которым удовлетворяют стороны треугольника (неравенство треугольника):

$a+b<c,$

$a+c<b,$

$c+b<a$

и углы

$\alpha +\beta +\gamma =180^{\circ}$

Примеры решения задач

ПРИМЕР 1

Задание

Известно, что длины двух сторон треугольника равны 4 см и 6 см, а угол между этими сторонами равен 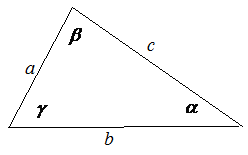$60^{\circ}$ . Найти третью сторону и углы треугольника.

Решение

Введем обозначения. Пусть $a=4$ см, $b=6$ см, тогда $\gamma =60^{\circ}$ . Сторону $c$ найдем из теоремы косинусов:

$c^{2} =a^{2} +b^{2} -2ab\cos \gamma =16+36-48\cdot \frac{1}{2} =28,$

откуда $c=2\sqrt{7}$ см.

Далее запишем теорему синусов и подставим известные данные:

$\frac{4}{\sin \alpha } =\frac{6}{\sin \beta } =\frac{2\sqrt{7}}{\sin 60^{\circ}}$

Следовательно,

$\sin \beta =\frac{6\cdot \frac{\sqrt{3}}{2}}{2\sqrt{7}} =\frac{3\sqrt{3}}{2\sqrt{7}} =\frac{3\sqrt{21}}{14} \Rightarrow \beta =\arcsin \frac{3\sqrt{21}}{14}$