Разносторонний треугольник
Определение и формулы разностороннего треугольника
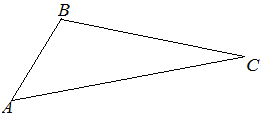
Для разностороннего треугольника справедливы следующие утверждения
- Сумма углов разностороннего треугольника равна
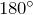 :
:
![Rendered by QuickLaTeX.com \[\angle A +\angle B +\angle C=180^{\circ} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-21dd8d483223ca92cf17888141530857_l3.png)
- Для разностороннего треугольника справедливо неравенство треугольника: сумма двух сторон всегда больше третьей стороны треугольника. Например, имеет место неравенство
- Все углы разностороннего треугольника имеют разную величину.
- Против большего угла треугольника лежит большая сторона.
![]()
Разносторонние треугольники бывают тупоугольные, остроугольные и прямоугольные.
Примеры решения задач
| Задание | В треугольнике |
| Решение | Найдем третий угол треугольника. Согласно теореме про сумму углов треугольника, имеем:
Поскольку против большего угла лежит большая сторона, то сторона |
| Ответ | Большая сторона – |
| Задание | Возможно ли существование треугольника со сторонами |
| Решение | В любом треугольнике сумма двух его сторон всегда больше третьей стороны (неравенство треугольника). Проверим это условие:
Поскольку последнее неравенство не выполняется в треугольнике, то треугольника с такими сторонами не существует. |
| Ответ | Нет |











