Разносторонний прямоугольный треугольник
Определение и формулы разностороннего прямоугольного треугольника
Треугольник называется прямоугольным, если один из его углов прямой.
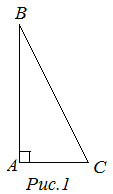
Стороны, образующие прямой угол называются катетами, а сторона, лежащая против прямого угла, называется гипотенузой.
Для разностороннего прямоугольного треугольника справедливы следующие утверждения:
- Теорема Пифагора. В разностороннем прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
- Сумма острых углов разностороннего прямоугольного треугольника равна
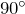 :
: - Гипотенуза треугольника больше каждого из катетов:
- Катет, лежащий против угла
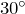 , равен половине гипотенузы.
, равен половине гипотенузы. - Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.
- Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности.
![]()
![]()
![]()
Примеры решения задач
| Задание | В прямоугольном треугольнике со сторонами |
| Решение | В прямоугольном треугольнике гипотенуза всегда больше каждого из катетов, поэтому она имеет длину 6 см, а катеты по 3 см и |
| Ответ |
| Задание | В прямоугольном треугольнике с катетами |
| Решение | Рассмотрим прямоугольный треугольник Поскольку центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, то ее радиус равен половине гипотенузы, т.е. |
| Ответ |











