Равнобедренный прямоугольный треугольник
Определение и формулы равнобедренного прямоугольного треугольника
Если катеты прямоугольного треугольника равны, то такой треугольник является равнобедренным прямоугольным треугольником.
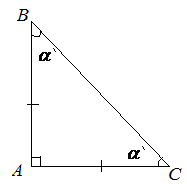
Для равнобедренного прямоугольного треугольника справедливы следующие утверждения:
- Острые углы равнобедренного прямоугольного треугольника равны по
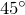 ;
; - Теорема Пифагора. В равнобедренном прямоугольном треугольнике квадрат гипотенузы равен удвоенному квадрату катета:
![Rendered by QuickLaTeX.com \[2AC^{2} =BC^{2}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-eb0080825292c884c1f21099c63f4e40_l3.png)
- Сумма острых углов такого треугольника равна
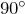 :
:
![Rendered by QuickLaTeX.com \[\angle B}+\angle C=90^{\circ} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e23370416057b3b4d3ad84eb6b4b552b_l3.png)
- Гипотенуза прямоугольного треугольника больше каждого их катетов:
![Rendered by QuickLaTeX.com \[AC<BC,\ AB<BC\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-5ea135fd84065df26bb33a440e26f7d8_l3.png)
- Две высоты равнобедренного прямоугольного треугольника совпадают с его катетами.
- Центр описанной окружности вокруг равнобедренного прямоугольного треугольника лежит на середине гипотенузы.
- Медиана равнобедренного прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является биссектрисой и высотой, а также радиусом описанной около этого треугольника окружности:
![]()
Тригонометрические соотношения в равнобедренном прямоугольном треугольнике
![]()
Площадь равнобедренного прямоугольного треугольника с катетом длины ![]() вычисляется по формуле:
вычисляется по формуле:
![]()
Примеры решения задач
| Задание | В равнобедренном прямоугольном треугольнике |
| Решение | Поскольку заданный в условии задачи треугольник равнобедренный и прямоугольный, значит, его катеты равны, то есть
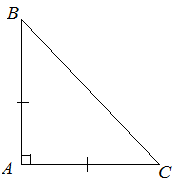
А квадрат гипотенузы тогда |
| Ответ |
| Задание | В равнобедренном треугольнике |
| Решение | Запишем для прямоугольного треугольника Так как этот треугольник равнобедренный, то Площадь равнобедренного прямоугольного треугольника равна половине квадрата катета, то есть |
| Ответ |











