Признаки равенства прямоугольных треугольников

Для прямоугольных треугольников можно сформулировать следующие признаки равенства треугольников:

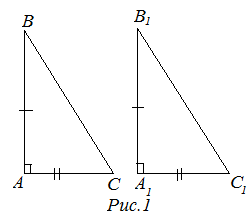
Первый признак равенства (по двум катетам)

1 признак (по двум катетам). Если два катета одного прямоугольного треугольника равны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники равны (рис. 1)

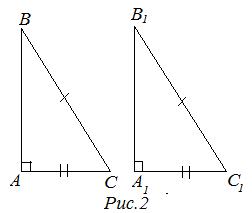
Второй признак равенства (по катету и гипотенузе)

2 признак (по катету и гипотенузе). Если катет и гипотенуза одного прямоугольного треугольника равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны (рис. 2).

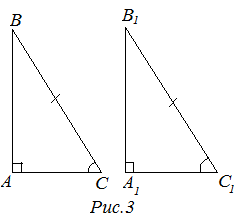
Третий признак равенства (по гипотенузе и острому углу)

3 признак (по гипотенузе и острому углу). Если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны (рис. 3).

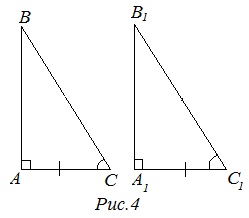
Четвертый признак равенства (по катету и острому углу)

4 признак (по катету и острому углу). Если катет и острый угол одного прямоугольного треугольника равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны (рис. 4).

Примеры решения задач

ПРИМЕР 1

Задание	В трапеции 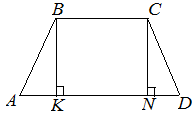опустили высоты и на основание , при этом . Доказать что трапеция – равнобокая.
Доказательство	В трапеции рассмотрим прямоугольные треугольники и . Стороны и равны между собой (как расстояния между параллельными прямыми), а по условию задачи. Получаем, что катеты треугольника равны катетам треугольника , а значит, эти треугольники равны (по первому признаку). Следовательно,     т.е. трапеция – равнобокая. Что и требовалось доказать.

ПРИМЕР 2

Задание	Доказать, что если в треугольнике две высоты равны, то этот треугольник является равнобедренным.
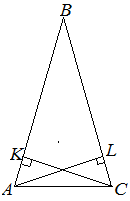
Доказательство	Рассмотрим треугольник . Проведем высоты и . По условию задачи они равны между собой. В прямоугольных треугольниках и угол – общий и катеты . Согласно признаку равенства прямоугольных треугольников (по катету и острому углу), треугольники и равны, а значит . Что и требовалось доказать.