Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Формулы по геометрии Треугольник Основание равнобедренного треугольника

Основание равнобедренного треугольника

ОПРЕДЕЛЕНИЕ

Треугольник называется равнобедренным, если две его стороны равны между собой. Равные стороны называются боковыми, а третья сторона – основанием.

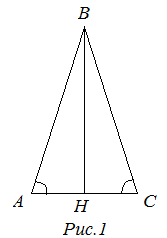
Основание равнобедренного треугольника

Свойства основания равнобедренного треугольника

Углы при основании равнобедренного треугольника равны между собой.
Высота, опущенная на основание равнобедренного треугольника, является одновременно биссектрисой и медианой.
Площадь равнобедренного треугольника равна половине произведения основания на высоту, проведенную к этому основанию:
$S=\frac{1}{2} ah_{a}$

Примеры решения задач

ПРИМЕР 1

Задание

Площадь равнобедренного треугольника $ABC$ равна $100$ см $^{2}$ . Найти основание треугольника, если высота, опущенная на основание, в два раза больше него.

Решение

Рассмотрим треугольник $ABC$ (рис. 1), в котором $AB=BC$ . Из вершины $B$ опустим высоту $BH$ на основание $AC$ . Пусть $AC=x$ , тогда $BH=2x$ . Следовательно,

$S=\frac{1}{2} \cdot x\cdot 2x=x^2 =100\Rightarrow x=10$

Получили, что основание $AC=10$ см $^{2}$ .

Ответ

$AC=10$ см $^{2}$

ПРИМЕР 2

Задание

В равнобедренном треугольнике $ABC$ найти основание $AC$ , если $\angle A=75^{\circ}$ , а $AB=BC=3$ см.

Решение

Поскольку треугольник $ABC$ – равнобедренный (рис. 1), то углы при основании равны, т.е.

$\angle A=\angle C=75^{\circ} ,$

Тогда, согласно теореме про сумму углов треугольника,

$\angle B=180^{\circ} -75^{\circ} -75^{\circ} =30^{\circ}$

Чтобы найти сторону $AC$ воспользуемся теоремой косинусов:

$AC^2 =AB^2 +BC^2 -2AB\cdot BC\cos \angle B=$

$=9+9-2\cdot 3\cdot 3\cdot \frac{\sqrt{3} }{2} =18-9\sqrt{3} =9\cdot \left(2-\sqrt{3} \right),$

откуда $AC=3\sqrt{2-\sqrt{3} }$ см.

Ответ

$AC=3\sqrt{2-\sqrt{3} }$ см

© SolverBook - онлайн сервисы для учебы, 2015

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Почта для связи: info@ru.solverbook.com

Выберите язык:

Сервисы

SolverBook