Окружность, вписанная в равнобедренный треугольник

Определение и формулы окружности, вписанной в равнобедренный треугольник

ОПРЕДЕЛЕНИЕ

Окружностью, вписанной в треугольник, называется окружность, которая касается всех трех сторон треугольника.

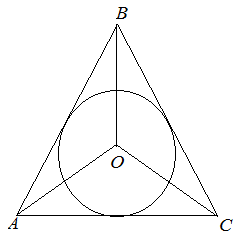
Окружность, вписанная в равнобедренный треугольник

Центром окружности, вписанной в треугольник, является точка пересечения биссектрис углов треугольника.

В любой треугольник можно вписать окружность, причем, только одну.

Рассмотрим окружность, вписанную в равнобедренный треугольник (тот, у которого две стороны равны между собой)

Радиус окружности, вписанной в равнобедренный треугольник можно вычислить по стандартной формуле

$r=\frac{S}{p} ,$

а также его можно выразить через стороны $a$ и $b$ следующим образом:

$r=\frac{b}{2} \sqrt{\frac{2a-b}{2a+b}}$

Примеры решения задач

ПРИМЕР 1

Задание

Найти боковую сторону равнобедренного треугольника, если его основание равно 6 см, а радиус вписанной окружности 4 см.

Пример окружности вписанной в равнобедренный треугольник

Решение

Рассмотрим равнобедренный треугольник $ABC$ с основанием $AC=10$ см. Воспользуемся формулой для радиуса вписанной окружности

$r=\frac{AC}{2} \sqrt{\frac{2AB-AC}{2AB+AC}}$

и подставим в нее известные данные

$r=\frac{10}{2} \sqrt{\frac{2AB-10}{2AB+10}} =4$

Из последнего равенства найдем $AB$ :

$\sqrt{\frac{2AB-10}{2AB+10}} =\frac{4}{5} \Rightarrow \frac{2AB-10}{2AB+10} =\frac{16}{25} \ \Rightarrow \ 50AB-250=32AB+160\ \Rightarrow$

$\Rightarrow \ AB=\frac{410}{18} =22\frac{7}{9} cm$

Ответ

$AB=22\frac{7}{9}$ см

ПРИМЕР 2

Задание

Найти радиус окружности, вписанной в равнобедренный треугольник, если точка касания окружности и боковой стороны делит ее на отрезки 8 см и 5 см, считая от вершины, противоположной основанию.

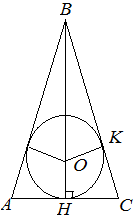
Решение

Рассмотрим равнобедренный треугольник $ABC$ с основанием $AC$ , в который вписана окружность. Точка $K$ – точка касания окружности и боковой стороны $BC$ такая, что $BK=8$ см, $KC=5$ см. Тогда

$BC=BK+KC=8+5=13 cm$