Окружность, описанная около прямоугольного треугольника

Определение и формулы описанной окружности прямоугольного треугольника

ОПРЕДЕЛЕНИЕ

Окружность, описанная около треугольника, содержит все вершины треугольника.

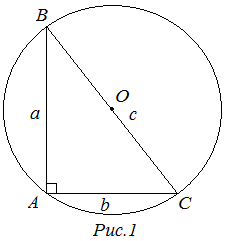
Окружность, описанная около прямоугольного треугольника

Центр описанной окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.

Рассмотрим прямоугольный треугольник $ABC$ . Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а радиус описанной окружности равен половине гипотенузы

$R=\frac{c}{2}$

Для прямоугольного треугольника справедлива теорема синусов:

$\frac{a}{\sin \alpha } =\frac{b}{\sin \beta } =c=2R,$

где $R$ – радиус описанной около прямоугольного треугольника окружности, $a,\ b$ – катеты этого треугольника, $c$ – его гипотенуза, $\alpha,\ \beta$ – острые углы треугольника.

Примеры решения задач

ПРИМЕР 1

Задание

В прямоугольном треугольнике один из катетов на 2 см больше другого. Найти площадь треугольника, если радиус описанной окружности равен 5 см.

Решение

Рассмотрим прямоугольный треугольник $ABC$ с $\angle A=90^{\circ}$ (рис. 1). Пусть катет $AB=x$ , тогда $AC=x+2$ . Поскольку радиус описанной окружности равен половине гипотенузы, то гипотенуза $BC=2\cdot 5=10cm$ . Запишем теорему Пифагора для рассматриваемого прямоугольного треугольника:

$AB^{2} +AC^{2} =BC^{2}$

или

$x^{2} +(x+2)^{2} =10^{2}$

Решая квадратное уравнение $2x^{2} +4x-96=0$ , получаем $x=6$ , т.е. $AB=6cm$ , а $AC=x+2=8$ см. Площадь прямоугольного треугольника равна половине произведения катетов, т.е.

$S=\frac{AB\cdot AC}{2} =\frac{1}{2} \cdot 6\cdot 8=24 cm ^{2}$

Ответ

$S=24$ см $^{2}$

ПРИМЕР 2

Задание

В прямоугольном треугольнике медиана 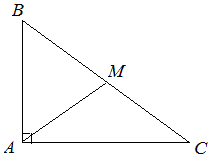$a$ , проведенная к гипотенузе, делит прямой угол в отношении $2:1$ . Найти катеты треугольника.

Пример окружности описанной около прямоугольного треугольника

Решение

Рассмотрим прямоугольный треугольник $ABC\ (\angle A=90^{\circ})$ и проведем медиану $AM$ . Так как центр окружности, описанной около прямоугольного треугольника, находится на середине гипотенузы, то медиана $AM$ является радиусом описанной окружности и

$AM=BM=MC=a$