Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Формулы по геометрии Треугольник Формула подобия треугольников

Формула подобия треугольников

Определение и формула подобия треугольников

ОПРЕДЕЛЕНИЕ

Треугольники называются подобными, если у них равны углы и пропорциональны стороны (рис. 1).

Формула подобия треугольников

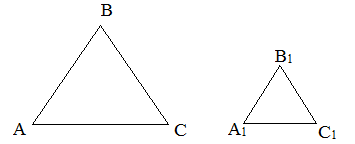
Рис.1

Рассмотрим подобные треугольники $ABC$ и $A_1 B_1 C_1$ . Соответствующие стороны этих треугольников пропорциональны, то есть

$\frac{AB}{A_1 B_1 } =\frac{BC}{B_1 C_1 } =\frac{AC}{A_1 C_1 } =k,$

где $k$ – коэффициент подобия треугольников.

Тогда отношение площадей двух подобных треугольников равно квадрату коэффициента подобия:

$\frac{S_{ABC} }{S_{A_1 B_1 C_1 } } =k^2$

Примеры решения задач

ПРИМЕР 1

Задание

Треугольники $ABC$ и $A_1 B_1 C_1$ подобны. Найти сторону $BC$ , если $B_1 C_1 =8$ см, площадь треугольника $ABC$ равна $64$ см $^{2}$ , а площадь треугольника $A_1 B_1 C_1$ равна $128$ см $^{2}$ .

Решение

Найдем отношение площадей треугольников $ABC$ и $A_1 B_1 C_1$

$\frac{S}{S_1 } =\frac{64}{128} =\frac{1}{2} ,$

т.е. коэффициент подобия

$k^2 =\frac{1}{2} \Rightarrow k=\frac{1}{\sqrt{2} }$

Тогда из подобия треугольников следует

$\frac{BC}{B_1 C_1 } =\frac{1}{\sqrt{2} } \Rightarrow BC=\frac{1}{\sqrt{2} } B_1 C_1 =4\sqrt{2} \ cm$

Ответ

$BC=4\sqrt{2}$ см

ПРИМЕР 2

Задание

Треугольники $ABC$ и $A_1 B_1 C_1$ подобны с коэффициентом подобия $k=4$ . Найти площадь треугольника $A_1 B_1 C_1$ , если $AB=5$ см, $BC=4$ см, $AC=7$ см.

Решение

Найдем площадь треугольника $ABC$ по формуле Герона:

$S=\sqrt{p(p-AB)(p-BC)(p-AC)} ,$

где $p=\frac{AB+BC+AC}{2} =\frac{5+4+7}{2} =8$ см – полупериметр треугольника $ABC$ . Тогда

$S=\sqrt{8\cdot (8-5)\cdot (8-4)\cdot (8-7)} =4\sqrt{6}$ см $^{2}$

Поскольку треугольники $ABC$ и $A_1 B_1 C_1$ подобные, то отношение их площадей равно квадрату коэффициента подобия, т.е.

$\frac{4\sqrt{6} }{S_1 } =4^2 =16,$

откуда $S_1 =\frac{\sqrt{6} }4 = 0,25 \sqrt{6}$ см $^{2}$

Ответ

$S_1 = 0,25 \sqrt{6}$ см $^{2}$

Читайте также:

Признаки подобия трапеций

Доказательство подобия треугольников

Подобные треугольники

Отношение площадей подобных треугольников

Свойства подобных треугольников

© SolverBook - онлайн сервисы для учебы, 2015

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Почта для связи: info@ru.solverbook.com

Выберите язык:

Сервисы

SolverBook