Боковая сторона равнобедренного треугольника

Определение и формулы боковых сторон равнобедренного треугольника

ОПРЕДЕЛЕНИЕ

Треугольник называется равнобедренным, если две его стороны равны.

Равные стороны называются боковыми сторонами, а третья – основанием треугольника.

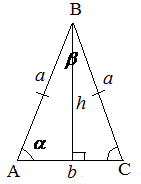
Формулы, выражающие боковую сторону равнобедренного треугольника через основание и угол при основании

$a=\frac{b}{2\cos \alpha } ,$

через высоту и угол при основании

$a=\frac{h}{\sin \alpha } ,$

через основание и угол между боковыми сторонами

$a=\frac{b}{2\sin \frac{\beta }{2}} ,$

где a – боковая сторона, $b$ – основание, $\alpha$ – угол при основании, $\beta$ – угол между боковыми сторонами.

ПРИМЕР 1

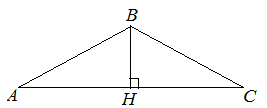
Задание

Найти боковую сторону равнобедренного треугольника, если основание треугольника равно 8 см, а высота, опущенная на основание 3 см.

Решение

Рассмотрим равнобедренный треугольник $ABC$ с основанием $AC=8$ см и высотой $BH=3$ см, которая также является медианой, т.е.

$AH=HC=4 cm$

Найдем длину боковой стороны $AB$ из прямоугольного треугольника $ABH$ по теореме Пифагора:

$AB=\sqrt{AH^{2} +BH^{2}} =\sqrt{16+9} =\sqrt{25} =5 cm$

Ответ

$AB=5$ см

ПРИМЕР 2

Задание

Площадь равнобедренного треугольника равна 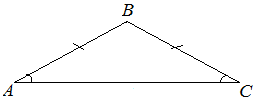$40\sqrt{3} cm ^{2}$ , а угол при основании $30^{\circ}$ . Найти боковую сторону треугольника.

Решение

Рассмотрим равнобедренный треугольник $ABC$ с основанием $AC$ . Поскольку углы при основании в равнобедренном треугольнике равны:

$\angle A=\angle C=30^{\circ} ,$

то можно найти угол между боковыми сторонами

$\angle B=180^{\circ} -2\cdot \angle AC=180^{\circ} -2\cdot 30^{\circ} =120^{\circ}$

Запишем формулу для площади треугольника по двум сторонам и углу между ними:

$S=\frac{1}{2} \cdot AB\cdot BC\cdot \sin \angle B=\frac{1}{2} \cdot AB^{2} \cdot \sin 120^{\circ} =40\sqrt{3} cm ^{2} ,$

откуда

$AB^{2} =\frac{2\cdot 40\sqrt{3}}{\sin 120^{\circ}} =\frac{80\sqrt{3}}{\sqrt{3}/2} =160\Rightarrow AB=4\sqrt{10} cm$

Ответ

$AB=4\sqrt{10}$ см

Понравился сайт? Расскажи друзьям!