Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Формулы по геометрии Формулы площади Площадь треугольника по трем сторонам

Площадь треугольника по трем сторонам

Определение и формула площади треугольника по трем сторонам

ОПРЕДЕЛЕНИЕ

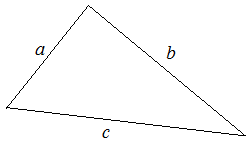
Треугольником называется фигура, состоящая из трех вершин и трех сторон, соединяющих эти вершины.

Треугольник

Существует много формул для вычисления площади треугольника.

Если известны длины всех сторон треугольника, то для вычисления площади треугольника удобно пользоваться формулой Герона:

$S=\sqrt{p(p-a)(p-b)(p-c)} ,$

где $a,\ b,\ c$ – стороны треугольника, а $p=\frac{a+b+c}{2}$ – его полупериметр.

Примеры решения задач

ПРИМЕР 1

Задание

Найти площадь треугольника со сторонами 5 см, 8 см и 11 см.

Решение

Для вычисления площади треугольника с известными длинами трех сторон применим формулу Герона. Найдем полупериметр треугольника

$p=\frac{5+8+11}{2} =12 cm$

Тогда

$S=\sqrt{p(p-a)(p-b)(p-c)} =\sqrt{12\cdot (12-5)\cdot (12-8)\cdot (12-11)} =4\sqrt{21} cm ^{2}$

Ответ

$S=4\sqrt{21}$ см $^{2}$

ПРИМЕР 2

Задание

Найти площадь треугольника 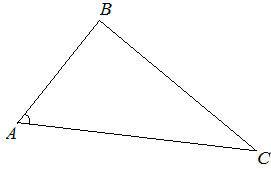$ABC$ , если известно, что $AB=3$ см, $BC=4$ см, $\angle A=60^{\circ}$ .

Площадь треугольника по трем сторонам

Решение

В треугольнике $ABC$ найдем длину третьей стороны $AC$ с помощью теоремы косинусов:

$BC^{2} =AB^{2} +AC^{2} -2\cdot AB \cdot AC\cos \angle A$

Подставим известные значения и получим:

$16=9+AC^{2} -2\cdot 3\cdot AC\cdot \frac{1}{2}$

или

$AC^{2} -3AC-7=0$

Решая квадратное уравнение относительно $AC$ , получим два корня 5 и –2. Нам подходит $AC=5$ см. Тогда полупериметр треугольника $ABC$ равен

$p=\frac{AB+BC+AC}{2} =\frac{3+4+5}{2} =6\ cm$

Для нахождения площади треугольника воспользуемся формулой Герона:

$S=\sqrt{p(p-AB)(p-BC)(p-AC)} =\sqrt{6\cdot (6-3)\cdot (6-4)\cdot (6-5)} =6\ cm ^{2}$

Ответ

$S=6$ см $^{2}$

© SolverBook - онлайн сервисы для учебы, 2015

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Почта для связи: info@ru.solverbook.com

Выберите язык:

Сервисы

SolverBook