Площадь трапеции
1. Площадь трапеции равна произведению полусуммы оснований ![]() и
и ![]() на высоту
на высоту ![]() (рис. 1):
(рис. 1):
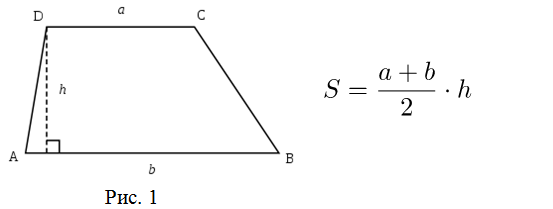
2. Если ![]() – диагонали трапеции, а
– диагонали трапеции, а ![]() – угол между ними (рис. 2), то площадь трапеции можно вычислить по формуле:
– угол между ними (рис. 2), то площадь трапеции можно вычислить по формуле:
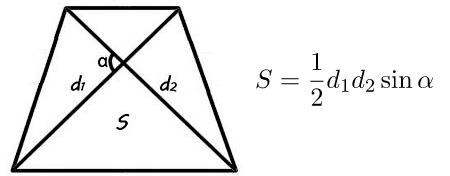
Примеры решения задач
| Задание | На рисунке 3 изображены параллельные прямые 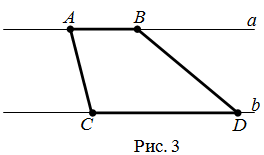
|
| Решение | Сделаем дополнительное построение. Построим отрезок 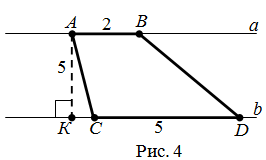
Отрезок |
| Ответ | Площадь трапеции равна |
| Задание | Вычислить площадь трапеции, одна диагональ которой равна |
| Решение | Найдем длину второй диагонали Тогда искомая площадь |
| Ответ | Площадь трапеции равна |











