Площадь ромба
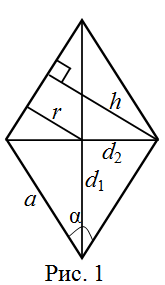
1. Площадь ромба равна произведению стороны на высоту, проведенную к этой стороне (рис. 1), то есть
![]()
2. Если известна сторона ромба (у ромба все стороны равны) и угол между сторонами (рис. 1), то площадь можно найти по следующей формуле:
![]()
3. Площадь ромба также равна полупроизведению диагоналей, то есть:
![Rendered by QuickLaTeX.com \[ S = \frac{d_{1}d_{2}}{2} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d13cf50e6f52307f0461a7e296844754_l3.png)
4. Если известен радиус ![]() окружности, вписанной в ромб (рис. 1), и сторона ромба
окружности, вписанной в ромб (рис. 1), и сторона ромба ![]() , то его площадь вычисляется по формуле:
, то его площадь вычисляется по формуле:
![]()
Примеры решения задач
| Задание | Найти площадь ромба с диагоналями 10 см и 6 см. |
| Решение | Искомая площадь равна половине произведения диагоналей, то есть
|
| Ответ | Площадь ромба равна |
| Задание | Найти площадь ромба, если его сторона равна 5, а большая диагональ – 8. |
| Решение | Сделаем рисунок (рис. 2).
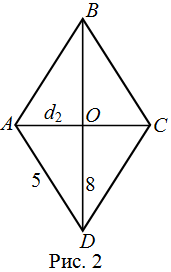
Обозначим меньшую диагональ ромба Рассмотрим прямоугольный треугольник А тогда искомая площадь |
| Ответ |






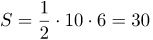 (см
(см




