Площадь окружности
Площадь окружности вычислить нельзя, окружность имеет лишь длину, но можно вычислить площадь круга, ограниченного окружностью заданного радиуса ![]() . Таким образом, задача сводиться к отысканию площади круга. Для площади круга радиуса
. Таким образом, задача сводиться к отысканию площади круга. Для площади круга радиуса ![]() имеют место следующие формулы
имеют место следующие формулы
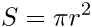 или
или 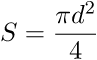
где ![]() – диаметр.
– диаметр.
Примеры решения задач
| Задание | Найти площадь участка плоскости, ограниченного окружностью радиуса |
| Решение | Часть плоскости ограниченной окружностью заданного радиуса есть круг радиуса
|
| Ответ |
| Задание | Вокруг квадрата со стороной |
| Решение | Сделаем рисунок (рис. 1).

Диагональ Подставляя значения
Далее для вычисления площади круга, ограниченного заданной окружностью, используем формулу:
|
| Ответ |






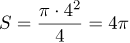 (см
(см




