Периметр трапеции
Формула периметра произвольной трапеции ![]() (рис. 1), в которой
(рис. 1), в которой ![]() , имеет вид:
, имеет вид:
![]()
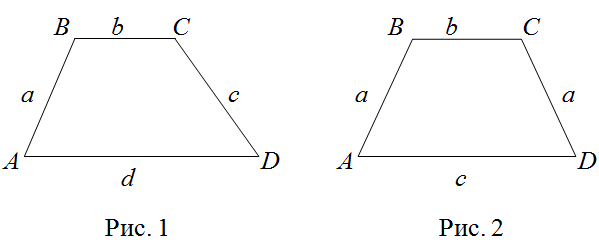
В случае, если трапеция ![]() – равнобокая (рис. 2), то есть
– равнобокая (рис. 2), то есть ![]() , формула для периметра трапеции примет вид:
, формула для периметра трапеции примет вид:
![]()
Примеры решения задач
| Задание | Найти периметр равнобокой трапеции |
| Решение | Обозначим Подставляя в неё исходные данные, получим
|
| Ответ | Периметр трапеции равен |
| Задание | Найти периметр прямоугольной трапеции, если её основания равны соответственно 9 дм и 6 дм, а меньшая боковая сторона равна 4 дм. |
| Решение | Сделаем рисунок (рис. 3).
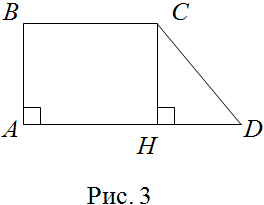
Обозначим Так как Далее рассмотрим треугольник Подставляя в последнее равенство известные значения катетов, получим
Периметр данной прямоугольной трапеции найдем по формуле В данном случае она примет вид: Подставляя длинны сторон трапеции в последнее равенство, получим
|
| Ответ |











