Формулы законов Кирхгофа

ОПРЕДЕЛЕНИЕ

Законы или правила Кирхгофа используют для упрощения расчетов сложных разветвленных цепей, которые могут содержать несколько замкнутых контуров, несколько источников ЭДС.

Законы Кирхгофа применяют для составления систем уравнений из которых находят силы тока, которые текут в элементах рассматриваемой цепи.

Любую точку цепи, в которой сошлись три или более проводников с токами называют узлом.

Формула первого закона Кирхгофа (правило узлов)

$\sum^N_{m=3}{I_m=0} \qquad (1)$

Выражение (1) означает, что алгебраическая сумма токов в любом узле цепи (при учете знаков токов) равна нулю. Знаки токов выбирают произвольно, но при этом следует считать, например, все токи, входящие в узлы положительными, тогда все токи, исходящие из узлов отрицательными. При решении одной задачи важно не путать знаки. Для того, чтобы не допускать ошибок со знаками при составлении суммы токов, часто на схемах силы токов изображают стрелками с направлениями от узла или к узлу.

Первый закон Кирхгофа — следствие закона сохранения заряда. Так как при постоянном токе никакая точка проводника (или участок цепи) не могут накапливать заряд. В противном случае токи не были бы постоянными.

Формула второго закона Кирхгофа (правило контуров)

$\sum_m{I_mR_m}=\sum_i{\varepsilon_i} \qquad(2)$

Формула (2) означает, что произведение алгебраической величины силы тока (I) на сумму вешних и внутренних сопротивлений всех участков замкнутого контура равно сумме алгебраических значений сторонних ЭДС ( $\varepsilon$ ) рассматриваемого контура.

Направление положительного обхода выбирают для всех контуров одинаковым в одной задаче. При составлении уравнений, используя правила Кирхгофа необходимо внимательно следить за расстановкой знаков токов и ЭДС. Знак ЭДС выбирается положительным, если при движении по контуру в положительном направлении первым встречается отрицательный полюс источника. (За положительное направление обхода контура принимают направление обхода цепи либо по часовой стрелке, либо против нее).

Втрое правило Кирхгофа является следствием обобщенного закона Ома.

Примеры решения задач по теме «Законы Кирхгофа»

ПРИМЕР 1

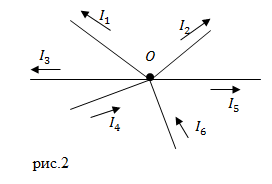
Задание

Запишите первый закон Кирхгофа для узла (O) который изображен на рис.1.

Решение

Будем считать положительным ток, который входит в узел. Такими токами для узла O станут токи:

$I_4;\ I_{6} \qquad(1.1)$

Из узла О выходят токи:

$I_1;\ I_{2} ;\ I_3;\ I_6\ \qquad(1.2)$

Значит, по принятому нами правилу токи из (1.2) будут отрицательными. В таком случае первое правило Кирхгофа нужно записать как:

$I_4+\ I_6-I_1-I_{2} -\ I_3-I_6=0$

Ответ

$I_4+\ I_6-I_1-I_{2} -\ I_3-I_6=0$

ПРИМЕР 2

Задание

На рис.2 изображена схема, в которой ЭДС источника 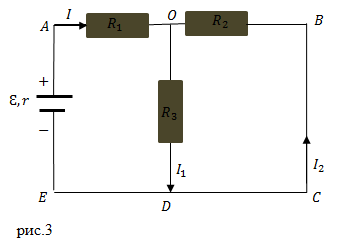$\varepsilon$ , сопротивления имеют величину: $R_1,\ R_2,\ R_3$ . Источник имеет сопротивление r. Какова величина силы тока $I_1$ ?

Решение

Рассмотрим токи в узле О. Будем считать токи, входящие в узел положительными, соответственно исходящие токи будут отрицательными Используем формулу первого правила Кирхгофа, для узла О имеем:

$I+I_2-I_1=0\ \qquad(2.1)$

Рассмотрим замкнутый контур AODE. За направление обхода контура примем движение по часовой стрелке. В соответствии со вторым правилом Кирхгофа получим следующее уравнение:

$\varepsilon=IR_1+I_1R_3+Ir\ \qquad(2.2)$

Рассмотрим еще один замкнутый контур нашей цепи OBCD для него используя второе правило Кирхгофа получим уравнение (обходим контур по часовой стрелке):

$0=-I_2R_2-I_1R_3 \qquad(2.3)$

Уравнений нам достаточно, так как мы имеем систему из трех линейно независимых уравнений:

$\left\{ \begin{array}{c} I+I_2-I_1=0\ \\ \varepsilon=IR_1+I_1R_3+Ir \\ 0=I_2R_2+I_1R_3 \end{array} \right.\ \qquad(2.4)$

Решим данную систему уравнений относительно искомого тока $I_1.$ Из первого уравнения выразим ток I:

$I=I_1-I_2\ \qquad(2.5)$

Из третьего уравнения системы получим ток $I_2$ :

$I_2=-\frac{I_1R_3}{R_2} \qquad(2.6)$

Подставим правые части выражений (2.5) и (2.6) вместо соответствующих токов во второе уравнение системы (2.4), выразим искомый ток $I_1$ :

$\varepsilon=\left(I_1+\frac{I_1R_3}{R_2}\right)R_1+I_1R_3+\left(I_1+\frac{I_1R_3}{R_2}\right)r\to I_1=\frac{\varepsilon}{R_1+\frac{R_1R_3}{R_2}+R_3+r+\frac{rR_3}{R_2}}$

Ответ

$I_1=\frac{\varepsilon}{R_1+\frac{R_1R_3}{R_2}+R_3+r+\frac{rR_3}{R_2}}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Формулы законов Кирхгофа

Формула первого закона Кирхгофа (правило узлов)

Формула второго закона Кирхгофа (правило контуров)

Примеры решения задач по теме «Законы Кирхгофа»