Формулы термодинамики

Определение и формулы термодинамики

ОПРЕДЕЛЕНИЕ

В термодинамике изучают самые общие законы и процессы преобразований энергии.

При этом считается, что любое тело имеет внутреннюю энергию (U), которая зависит от его температуры:

$U=\frac{i}{2}\frac{m}{\mu }RT\ \qquad(1)$

где i – число степеней свободы молекулы; m – масса; $\mu$ – молярная масса; $R=8,31\ \frac{J}{mol\cdot K}$ – универсальная газовая постоянная; T – температура по абсолютной шкале.

При теплообмене количество теплоты (Q) служит мерой изменения внутренней энергии. Количество теплоты, которое получает тело массы m при увеличении его температуры на величину равную $\Delta \ t (^{\circ}C)$ , равно:

$\Delta Q=mc\Delta \ t \qquad(2)$

где $c=\frac{C}{m}$ – удельная теплоемкость вещества. В общем случае теплоемкость тела (C) определена как:

$C=\frac{\delta Q}{dT} \qquad(3)$

В соответствии с первым началом термодинамики, теплота, которую получает термодинамическая система ( $\Delta Q$ ), расходуется ей на совершение работы (A) и изменение ее внутренней энергии ( $\Delta U$ ):

$\Delta Q=A+\Delta U\ \qquad(4)$

Для элементарного изменения состояния термодинамической системы первый закон термодинамики записывают как:

$\delta Q=\delta A+dU\ \qquad(5)$

или:

$CdT=pdV+dU\ \qquad(6)$

где p – давление; $dV$ – элементарное изменение объема.

Термодинамическим коэффициентом полезного действия (КПД) ( $\eta$ ) называют отношение работы (A), которое совершает рабочее тело к количеству теплоты ( $Q^+$ ), которое получает данное тело:

$\eta =\frac{A}{Q^+}=\frac{Q^+-Q^-}{Q^+} \qquad(7)$

где $Q^-$ — количество теплоты, отданное рабочим телом холодильнику.

Для цикла Карно, который состоит из двух изотерм и двух адиабат и проводится с идеальным газом КПД равно:

$\eta =\frac{T_1-T_2}{T_1} \qquad(8)$

где $T_1$ – температура нагревателя; $T_2$ – температура холодильника.

Энтропия в термодинамике

Энтропией называют функцию состояния термодинамической системы, элемент которой в обратимом процессе равен:

$dS=\frac{\delta Q}{T} \qquad(9)$

В соответствии со вторым началом термодинамики в необратимом элементарном процессе изменение энтропии:

$dS>\frac{\delta Q}{T}\left(10\right)$

Для адиабатного процесса выражение (10) имеет вид:

$dS\ge 0\ \left(11\right)$

где знак равно относится к обратимому процессу. Выражение (11) – математическая запись второго начала термодинамики (Следует помнить, что рассматривается замкнутая система).

Работа в термодинамике вычисляется как:

$A=\int^{V_2}_{V_1}{pdV} \qquad (12)$

где $V_1$ – начальный объем системы; $V_2$ – конечный объем. Работа считается большей нуля, если работу выполняет система (газ) над внешними силами.

Примеры решения задач по теме «Термодинамика»

ПРИМЕР 1

Задание

Дайте характеристики простейших изо процессов для идеального газа, приведите законы связывающие параметры их состояний, запишите первое начало термодинамики применительно к данным процессам.

Решение

1) Изохорный процесс: $m=const;\ V=const$ . Параметры состояния процесса связывает закон Шарля:

$\frac{p}{T}=const\ \qquad(1.1)$

Работа в изохорном процессе равна нулю ( $A=0;\ \delta A=0$ ). Первое начало термодинамики запишем как:

$\Delta Q=\Delta U=C_V\Delta T;\ \delta Q=C_VdT\ \qquad(1.2)$

2) Изобарный процесс: $m=const;\ p=const$ . Параметры состояния процесса связывает закон Гей-Люссака:

$\frac{V}{T}=const\ \qquad(1.3)$

Работа в изобарном процессе равна:

$A=p\Delta V;\ \delta A=pdV\ \qquad(1.4)$

Первое начало термодинамики для изобарного процесса:

$\Delta Q=A+\Delta U=C_p\Delta T;\ \delta Q=C_pdT\ \qquad(1.5)$

3) Изотермический процесс определен как процесс при : $m=const;\ T=const$ . Параметры состояния процесса связывает закон Бойля — Мариотта:

$pV=const\ \qquad(1.6)$

Работа в изотермическом процессе равна:

$\delta A=pdV;\ A=\nu RTln(\frac{V_2}{V_1})\ \qquad(1.7)$

Изменение внутренней энергии в изотермическом процессе равно нулю, поэтому первое начало термодинамики для него представлено формулой:

$\Delta Q=A;\ \delta Q=\delta A\ \qquad(1.8)$

ПРИМЕР 2

Задание

На рис. 1 заданы два циклических процесса. Найдите отношения работ (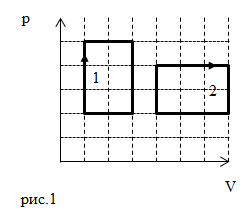 $\frac{A_1}{A_2}$ ), производимых газом.

Решение

По определению работа газа в термодинамике равна:

$A=\int^{V_2}_{V_1}{pdV} \qquad (2.1)$

Исходя из свойства интеграла, получим, что работа – равна площади криволинейной трапеции, которая задана подынтегральным выражением. Но, следует учесть, что в круговом процессе работу выполняет газ и работа выполняется над газом, когда его объем уменьшают от максимального (в рассматриваемом процессе) до первоначального. Получается, что результирующая работа, выполняемая газом в круговом процессе, равна площади фигуры, которая ограничена замкнутой кривой цикла, если цикли представлен в осях $p(V).$ В нашем случае (рис.1) в первом и втором случаях – это прямоугольники. Длины сторон наших прямоугольников равны, следовательно, равны их площади, получаем, что:

$A_1=A_2$

Ответ

$\frac{A_1}{A_2}=1$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Формулы термодинамики

Определение и формулы термодинамики

Энтропия в термодинамике

Примеры решения задач по теме «Термодинамика»