Формулы неподвижного блока
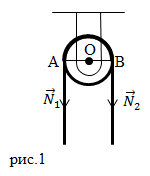
Блок на рис.1 будет находиться в равновесии, если силы ![]() , так как плечи этих сил одинаковы (ОА=ОВ). Блок – это рычаг, который имеет равные плечи. Блок, который представлен на рис.1 не дает выигрыша в силе, однако он позволяет изменять направление действия силы. Тянуть за веревку, которая идет сверху обычно удобнее, чем за веревку, которая идет снизу.
, так как плечи этих сил одинаковы (ОА=ОВ). Блок – это рычаг, который имеет равные плечи. Блок, который представлен на рис.1 не дает выигрыша в силе, однако он позволяет изменять направление действия силы. Тянуть за веревку, которая идет сверху обычно удобнее, чем за веревку, которая идет снизу.
Допустим, что через блок, который является сплошным диском радиусом R и массой m, перекинута нерастяжимая нить, которая неспособна скользить по блоку. На нити повесили грузы массами ![]() и
и ![]() (рис.2). Определим, каковы ускорения грузов (
(рис.2). Определим, каковы ускорения грузов (![]() и
и ![]() ) и разность натяжения нитей
) и разность натяжения нитей ![]() .
.
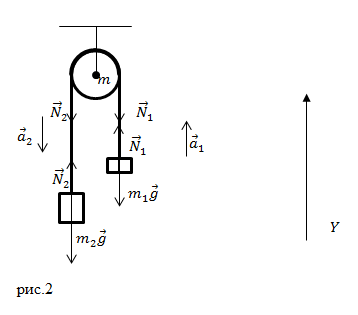
Уравнение движение груза номер один будет иметь вид:
![]()
В проекции на ось Y, получим:
![]()
Для второго груза сразу напишем уравнение движения в проекции на ось Y\^
![]()
Так как мы считаем нить нерастяжимой, то ускорения первого и второго грузов одинаковы по модулю:
![]()
Учтем равенство (4), сложим уравнения (2) и (3), получим:
![]()
Далее необходимо рассмотреть уравнение вращательного движения блока. Моменты сил, которые создаются силами натяжения нити, имеют противоположные знаки, поэтому запишем:
![]()
где J – момент инерции блока; ![]() – угловое ускорение блока. Выражение (6) преобразуем к виду:
– угловое ускорение блока. Выражение (6) преобразуем к виду:
![]()
Из формул (5) и (7) имеем:
![]()
Если можно в задаче массу блока не учитывать (момент инерции блока мал), то можно считать, что выполняется условие:
![]()
то разность натяжений нитей существенно меньше разностей силы тяжести грузов. Для невесомого блока будем иметь следующие формулы:
![]()
Примеры решения задач по теме «Неподвижный блок»
| Задание | Через блок, имеющий массу |
| Решение | Так как нить нерастяжима, то грузы будут двигаться с равными по величине ускорениями, но противоположно направленными. Так как по условию задачи блок имеет массу, для решения задачи используем формулу:
Момент инерции (J) сплошного диска относительно оси, проходящей через его центр масс равен: Подставим выражение (1.2) в формулу (1.1), имеем: Вычислим ускорения грузов: |
| Ответ | |
| Задание | Машину Атвуда используют для рассмотрения законов равноускоренного движения тел. Она представляет собой два груза с разными массами, которые подвешены на почти невесомой нити, которая перекинута через неподвижный блок. Чему равны силы натяжения нити, если блок считать невесомым? Массы грузов равны 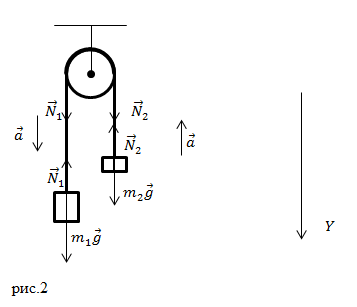
|
| Решение | Если блок считаю невесомым, то:
Из рис.2 имеем: При этом ускорение грузов равно: Получим: |
| Ответ | |











