Формулы адиабатического процесса

ОПРЕДЕЛЕНИЕ

Процесс, происходящий без обмена с окружающей средой теплотой, называют адиабатическим.

Это идеализированный процесс. Близкими к адиабатическим процессам являются процессы, происходящие с большой скоростью.

Формулу, которая описывает адиабатический процесс в идеальном газе легко получить из первого начала термодинамики, которое для этого процесса принимает вид:

$\delta A=-dU\ \qquad(1)$

уравнение (1) означает то, что работа в адиабатическом процессе совершается за счет уменьшения внутренней энергии системы. По определению работы в термодинамическом процессе, имеем:

$\delta A=pdV\ \qquad(2)$

где p – давление газа; $dV$ – малое изменение объема системы. По определению внутренняя энергия:

$dU=\frac{i}{2}R\nu dT\ \qquad(3)$

где i – число степеней свободы молекулы; $\nu$ – количество вещества; R – универсальная газовая постоянная; $dT$ – элементарное изменение температуры.

Учитывая выражения (2) и (3) первое начало термодинамики для адиабатного процесса, запишем как:

$pdV=-\frac{i}{2}\nu RdT\ \to dT=-\frac{2pdV}{i\cdot \nu\cdot R} \qquad(4)$

Состояние идеального газа можно описать уравнением Менделеева – Клапейрона:

$pV=\nu RT \qquad(5)$

Из (5), получаем:

$pdV+Vdp=\nu RdT\ \qquad(6)$

Подставим вместо $dT$ в формулу (6) правую часть выражения (4):

$pdV+Vdp=-\nu R\frac{2pdV}{i\cdot \nu \cdot R}=-\frac{pdV}{i}\to \frac{pdV+Vdp}{pdV}=-\frac{2}{i}\to \frac{dp}{p}=-\gamma \frac{dV}{V} \qquad(7)$

где для идеального газа $\gamma =\frac{2+i}{i}$ – показатель адиабаты (или коэффициент Пуассона). Из полученного дифференциального уравнения имеем:

$pV^{\gamma }=const\ \qquad(8)$

Уравнение (7) можно считать формулой, которая описывает адиабатический процесс (уравнение адиабаты, уравнение Пуассона). Формулы для адиабатического процесса можно легко получить в других параметрах: (p(T) или V(T)).

$\frac{p_2}{p_1}={\left(\frac{V_1}{V_2}\right)}^{\gamma };\ \frac{T_2}{T_1}={\left(\frac{V_1}{V_2}\right)}^{\gamma -1};\ \frac{T_2}{T_1}={\left(\frac{p_2}{p_1}\right)}^{\frac{\gamma -1}{\gamma }} \qquad(9)$

Диаграмма адиабатического процесса в осях p(V) является гиперболой.

Адиабатический процесс происходит при постоянной теплоемкости, равной нулю.

Примеры решения задач по теме «Адиабатический процесс»

ПРИМЕР 1

Задание

Газ расширяется и переходит из одного и того же состояния с объемом $V_1$ в состояние $V_2$ . В первом случае в изотермическом процессе, во втором случае в адиабатном процессе. Изобразите процессы на графике, в осях $p(V)$ . В каком случае работа газа будет больше?

Решение

Формула, описывающая изотермический процесс в параметрах $p(V):$

$pV=const\ \qquad(1.1)$

Адиабатический процесс задает формула: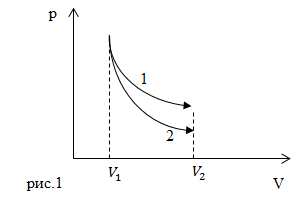

$pV^{\gamma }=const\ \qquad(1.2)$

где $\gamma =\frac{2+i}{i}=1+\frac{2}{i}$ – показатель адиабаты, является величиной, большей единицы, следовательно, на графике в осях $p(V)$ адиабата идет круче изотермы. Это мы отобразим на графике рис.1

На рис. 1 изображен изотермический процесс расширения идеального газа от объема $V_1$ до объема $V_2$ , это линия обозначенная цифрой 1. Вторая линия – это адиабата, которая так же обозначает расширение газа от объема $V_1$ до объема $V_2$ . Работа газа при изменении его объема равна:

$A=\int^{V_2}_{V_1}{pdV} \qquad (1.1)$

Если рассматривать процесс изменения объема газа в осях $p(V)$ , то в соответствии с геометрическим смыслом интеграла, работа будет численно равна площади криволинейной трапеции, которую ограничивают график процесса и вертикальные изохоры $V_1$ и $V_2$ . Площадь фигуры, которая получается в изотермическом процессе явно больше (рис.1), чем площадь трапеции, которую образует адиабата и соответствующие изохоры. Значит сделаем вывод о том, что работа в изотермическом процессе больше, чем работа в адиабатном процессе при заданных условиях.

Ответ

Работа в изотермическом процессе больше.

ПРИМЕР 2

Задание

В сосуде под поршнем находится идеальный газ при температуре $T_1=600$ K. Газ расширился адиабатически, при этом его объем увеличился в пять раз. Чему равна конечная температура газа ( $T_2$ ), если это был водород?