Формула второго закона Кирхгофа

Какой бы сложной не была электрическая цепь, она имеет элементы двух видов: узлы и замкнутые контуры. Узлом цепи называют точку разветвления цепи, в которой сходятся три или более проводника с током. Расчеты в любой самой сложной цепи можно провести, используя закон Ома и закон сохранения заряда. Для упрощения расчетов цепей постоянного тока используют правила (законы) Кирхгофа, которые позволяю составить линейные уравнения вычисления сил токов, текущих в элементах цепи.

ОПРЕДЕЛЕНИЕ

Второе правило Кирхгофа (правило контуров) – это следствие закона Ома. Если в изолированной замкнутой цепи присутствует источник ЭДС, то сила тока в этой цепи становится такой, что падение напряжения на внешнем сопротивлении и сопротивлении источника, равна ЭДС источника.

Падение напряжения это произведение силы тока на сопротивление ( $IR$ ). Если в цепи источников ЭДС будет несколько, то следует ЭДС суммировать, учитывая знаки. ЭДС принято считать положительной, если при обходе контура первым встречается отрицательный полюс источника. Направление обхода контура выбирают произвольно, (по часовой стрелке или против нее). Один раз выбрав направление обхода контура при решении задачи не следует его изменять.

Теперь к самой формуле, отображающей второй закон Кирхгофа:

$\sum_k{I_kR_k}=\sum_m{\varepsilon_m} \qquad (1)$

Формула второго закона Кирхгофа говорит о том, что сумма произведений силы токов (I) (с учетом знака) на внешние и внутренние сопротивления всех участков замкнутого контура равны сумме величин ЭДС ( $\varepsilon$ ) источников, которые включены в данный контур (суммирование ЭДС происходит с учетом знаков). При составлении и уравнений с использованием формулы второго закона Кирхгофа необходимо внимательно следить за расстановкой знаков токов и ЭДС.

Система уравнений, которая получается при использовании первого и второго правил Кирхгофа является полной и дает возможность отыскать все токи. При составлении уравнений, используя правила Кирхгофа, надо следить за тем, чтобы новое уравнение имело хотя бы одну величину, которая еще не вошла в предыдущие уравнения. Кроме того, необходимо, чтобы система уравнений имела число уравнений равное количеству неизвестных.

Второе правило Кирхгофа следует из того, что электрическое напряжение по замкнутому контуру равно нулю, то есть это правило является следствием основного свойства электростатического поля, которое заключается в том, что работа поля при движении заряда по замкнутой траектории равна нулю.

Примеры решения задач по теме «Второй закон Кирхгофа»

ПРИМЕР 1

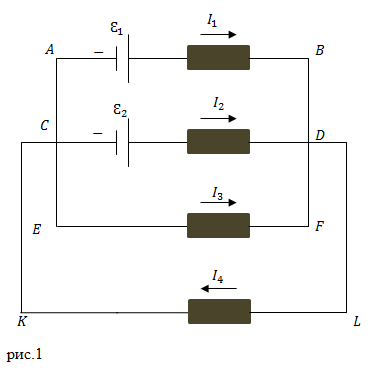
Задание

Рассмотрите схему рис.1. Выберите независимые контуры. Примените второе правило Кирхгофа для составления уравнений для избранных контуров. Считайте, что сопротивления источников ЭДС и проводов можно не учитывать.

Решение

Выберем направления токов, как они указаны на рис.1. Направление обхода контуров зададим по часовой стрелке. В нашей схеме имеются шесть замкнутых контуров. Из них три независимых. Для того чтобы количество независимых контуров отыскать, следует использовать такое правило: контуры выбирают так, что в каждый новый контур входит хотя бы одна новая ветка, которая не была учтена в уже рассмотренных контурах. Напомним о том как правильно расставить знаки во втором правиле Кирхгофа:

Если ток имеет направление, совпадающее с направлением обхода контура, то его произведение на соответствующее сопротивление войдет в уравнение со знаком плюс.
Если ЭДС повышает потенциал в направлении обхода контура (при обходе контура идем от минуса к плюсу внутри источника), то ЭДС войдет в уравнение со знаком плюс.

В качестве независимых контуров примем контуры: $CABDC;\ ABFEA;\ CEFDLKC.$

Для контура $CABDC$ второе правило Кирхгофа даст уравнение:

$I_1R_1-I_2R_2=\varepsilon_1-\varepsilon_2 \qquad(1.1)$

Для контура $ABFEA$ запишем:

$I_1R_1-I_3R_3=\varepsilon_1 \qquad(1.2)$

Используя правило контуров для $CEFDLKC$ получаем:

$I_3R_3+I_4R_4=0 \qquad(1.3)$

Ответ

Контур $CABDC,$ уравнение: $I_1R_1-I_2R_2=\varepsilon_1-\varepsilon_2.$ Контур $ABFEA$ , уравнение: $I_1R_1-I_3R_3=\varepsilon_1.$ Контур $CEFDLKC$ , уравнение: $I_3R_3+I_4R_4=0$

ПРИМЕР 2

Задание

Рассмотрите еще три контура для схемы на рис. 1, убедитесь, что Вы получите уравнения, которые будут связаны с имеющимися уравнениями, полученными в примере 1.

Решение

Рассмотрим контуры (рис.1) такие как: $CDFEC$ , для него правило контуров даст уравнение:

$I_2R_2-I_3R_3=\varepsilon_2 \qquad(2.1)$

Следующий контур возьмем: $ABDLKCA$ из второго правила Кирхгофа для этого контура имеем:

$I_1R_1+I_4R_4=\varepsilon_1 \qquad(2.2)$

Рассмотрим контур $CDLKC$ , из второго закона Кирхгофа получим:

$I_2R_2+I_4R_4=\varepsilon_2 \qquad(2.3)$

Обратимся к системе уравнений, которую мы получили в первом примере:

$\left\{ \begin{array}{c} I_1R_1-I_2R_2=\varepsilon_1-\varepsilon_2, \\ I_1R_1-I_3R_3=\varepsilon_1, \\ I_3R_3+I_4R_4=0. \end{array} \right. \qquad(2.4)$

Уравнение (2.1) можно получить, если из второго уравнения системы (2.4) вычесть первое уравнение этой же системы:

$I_1R_1-I_3R_3-\left(I_1R_1-I_2R_2\right)=\varepsilon_1-\left(\varepsilon_1-\varepsilon_2\right)\to I_2R_2-I_3R_3=\varepsilon_2$

Это означает, что уравнения (2.1) и первые да уравнения системы (2.4) линейно зависимы.

Уравнение (2.2) можно получить как линейную комбинацию уравнений второго и третьего уравнения системы (2.4), а именно их сумму:

$I_1R_1-I_3R_3+I_3R_3+I_4R_4=\varepsilon_1\to I_1R_1+I_4R_4=\varepsilon_1$

Уравнение (2.3) получается, если сложить последние два уравнения системы (2.4) и из них вычесть первое уравнение:

$I_1R_1-I_3R_3+I_3R_3+I_4R_4-\left(I_1R_1-I_2R_2\right)=\varepsilon_1-\left(\varepsilon_1-\varepsilon_2\right)\to I_2R_2+I_4R_4=\varepsilon_2$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Формула второго закона Кирхгофа

Примеры решения задач по теме «Второй закон Кирхгофа»