Формула силы притяжения

ОПРЕДЕЛЕНИЕ

Сила гравитационного притяжения между телами равна произведению гравитационной постоянной и масс обоих объектов, делённому на квадрат расстояния между ними.

$F = G \frac{m_{1} \cdot m_{2}}{R^{2}}$

Здесь $F$ – сила притяжения, $G$ – гравитационная постоянная, $m_{1}, m_{2}$ — массы объектов, $R$ – расстояние между центрами масс объектов.

Единица измерения силы – Н (ньютон).

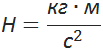
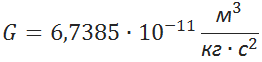
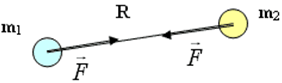
Сила гравитации возникает между любыми объектами в Вселенной, обладающими массой. Будучи приложенной к каждому объекту, она направлена на другой, причём модуль этой силы равен для обоих объектов:

Для тела, находящегося на поверхности Земли, формула упрощается, так как масса Земли и расстояние от центра Земли до поверхности известно:

$F = mg$

Где $g \approx 9,8$ м/с $^{2}$ . $g$ называют ускорением свободного падения.

Примеры решения задач по теме «Сила притяжения»

ПРИМЕР 1

Задание	Найти силу притяжения между объектами, массами 100т и 1000т, находящимися на расстоянии 3 км.
Решение	Напомним, что 1 т = 1000 кг, а 1 км = 1000 м. Подставим исходные данные в формулу: $F = G \frac{m_{1} \cdot m_{2}}{R^{2}} = 6,7385 \cdot 10^{-11} \frac{100 \cdot 10^{3} \cdot 1000 \cdot 10^{3}}{(3 \cdot 1000)^{2}} = 7,4872 \cdot 10^{-5} (H)$
Ответ	Сила гравитации равна $F = 7,4872 \cdot 10^{-5} (H)$ .

ПРИМЕР 2

Задание

Некое тело массой $m = 4 \cdot 10^{7}$ кг находится на высоте $1000$ км над Землёй. Во сколько раз изменится сила притяжения к Земле, если это тело поместить на её поверхность? Масса Земли равна $m_{3} = 5,972 \cdot 10^{24}$ кг, радиус Земли $R_{3} = 6,371 \cdot 10^{6}$ м.

Решение

Вспомним, что 1 км = 1000 м. Пусть в первом случае высота тела над Землёй равна $h$ , а сила притяжения Земли равна $F_{1}$ . Найдём её по формуле:

$F_{1} = G \frac{m \cdot m_{3}}{(h + R_{3})^{2}}$

Во втором случае тело находится на Земле, значит силу тяжести $F_{2}$ найти проще:

$F_{2} = mg$

Значит:

$\frac{F_{1}}{F_{2}} = \frac{G \frac{m \cdot m_{3}}{(h + R_{3})^{2}}}{mg} = \frac{G (m \cdot m_{3})}{mg \cdot (h + R_{3})^{2}}$

$\frac{F_{1}}{F_{2}} = \frac{6,7385 \cdot 10^{-11} \cdot (4 \cdot 10^{7} \cdot 5,792 \cdot 10^{24})}{4 \cdot 10^{7} \cdot 9,8 \cdot (10^{6} + 6,371 \cdot 10^{6})^{2}} = 0,733$

Ответ

Соотношение сил составило $0,733$ .

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Формула силы притяжения

Примеры решения задач по теме «Сила притяжения»