Формула силы инерции

Для того чтобы второй закон Ньютона выполнялся в неинерциальных системах отсчета в дополнение к силам, которые действуют на тела вводят силы инерции.

Определение и формула силы инерции

ОПРЕДЕЛЕНИЕ

Силой инерции называют силу, которая вводится только потому, что система координат, в которой происходит рассмотрение движения тел, является неинерциальной.

Возникновение сил инерции не связано с действием каких-либо тел. Напомним, что неинерциальными системами отсчета являются любые системы, движущейся с ускорением относительно инерциальных систем.

Третий закон Ньютона для сил инерции не выполняется.

Пусть ускорение тела относительно инерциальной системы отсчета равно ${\overline{a}}_a$ . Обычно такое ускорение называют абсолютным, при этом ускорение тела относительно неинерциальной системы отсчета носит название относительного ( ${\overline{a}}_o$ ). Второй закон Ньютона для инерциальной системы отсчета запишем как:

$m{\overline{a}}_a=\overline{F} \qquad(1)$

где $\overline{F}$ – равнодействующая сила, приложенная к телу массы m. В неинерциальной системе отсчета:

$m{\overline{a}}_o\ne \overline{F} \qquad(2)$

поскольку:

${\overline{a}}_o\ne {\overline{a}}_a \qquad(3)$

Добавим к правой части выражения (2) силы инерции, так чтобы выполнялся второй закон Ньютона в неинерциальной системе отсчета:

$m{\overline{a}}_o=\overline{F}+{\overline{F}}_i \qquad(4)$

В таком случае получим, что сила инерции равна:

${\overline{F}}_i=m\left({\overline{a}}_o-{\overline{a}}_a\right) \qquad(5)$

Формула (5) для силы инерции дает верное описание движения в неинерциальной системе отсчета. При этом нахождение разности относительного и абсолютного ускорений является кинематической задачей. Ее можно решить, если известен характер движения неинерциальной системы отсчета относительно инерциальной.

Системы отсчета, движущиеся прямолинейно с постоянным ускорением

Система отсчета, которая перемещается прямолинейно с постоянным ускорением – это простейший случай неинерциальной системы. Рассмотрим неинерциальную систему отсчета, которая движется прямолинейно с постоянным ускорением ${\overline{a}}_p$ (переносное ускорение) относительно инерциальной системы отсчета. Тогда:

${\overline{a}}_a={\overline{a}}_o+{\overline{a}}_p\ \qquad(6)$

Согласно формуле (5) сила инерции равна:

${\overline{F}}_i=-m{\overline{a}}_p \qquad(7)$

Вращающаяся система отсчета

Рассмотрим систему отсчета, вращающуюся относительно неподвижной оси с постоянной скоростью $\omega$ . Для тела находящегося в состоянии покоя в такой системе отсчета формулу для силы инерции можно записать как:

${\overline{F}}_i=m{\omega }^2\overline{r} \qquad(8)$

где $\overline{r}$ – радиус-вектор, по величине равный расстоянию от оси вращения до рассматриваемого тела, направленный от центра к телу. Сила инерции (8) называется центробежной силой инерции.

Все тела на поверхности Земли испытывают действие центробежной силы инерции.

Отметим, что всякую задачу можно решить в инерциальной системе отсчета. Применение неинерциальных систем продиктовано соображениями удобства применения неинерциальных систем.

Примеры решения задач по теме «Сила инерции»

ПРИМЕР 1

Задание

Какова сила нормального давления тела (вес) на поверхность Земли, если тело неподвижно, имеет массу m. Находится на широте $\varphi$ . Радиус Земли считать равным R.

Решение

Сделаем рисунок.

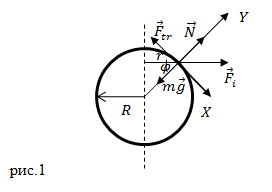
Свяжем систему отсчета с Землей. На груз в этой системе отсчета действуют силы: сила тяжести ( $m\overline{g}$ ); сила реакции опоры ( $\overline{N}$ ); сила трения покоя ( ${\overline{F}}_{tr}$ ). Кроме этих сил, так как систему отсчета связанную с Землей в нашем случае инерциальной считать не будем, действует центробежная сила инерции ( ${\overline{F}}_i$ ). Формулу для расчета силы инерции возьмем:

${\overline{F}}_i=m{\omega }^2\overline{r} \qquad(1.1)$

где $r=R{\cos \varphi } -$ радиус траектории (окружности) по которой движется груз.

Систему координат выберем так, что ее начало совпадет с центром тела, ось Y будет перпендикулярна поверхности Земли, ось X – касательная к поверхности Земли (см. рис.1). Так как тело не движется относительно Земли, то второй закон Ньютона запишем как:

$m\overline{g}+\overline{N}+{\overline{F}}_{tr}+{\overline{F}}_i=0\ \qquad(1.2)$

В проекциях на оси X и Y выражения (1.2), учитывая (1.1) имеем:

$\left\{ \begin{array}{c} X:\ -mg+N+m{\omega }^2R\cos \varphi } =0, \\ Y:\ -F_{tr}+m{\omega }^2R{\sin \varphi } \cos \varphi =0} \end{array} \right.\ \qquad(1.3)$

Так как вес тела (P) по величине равен (N), выразим его из первого уравнения системы (1.3), получим:

$N=mg-m{\omega }^2R\cos \varphi } \qquad (1.4)$

Ответ

$P=mg-m{\omega }^2R\cos \varphi \ }$

ПРИМЕР 2

Задание

Рассмотрите результаты решения задачи в первом примере и ответе на вопросы:

В каком месте Земли сила трения покоя равна нулю?
В каких местах Земли сила трения максимальна?
Где вес тела равен силе тяжести?

Решение

Для ответа на первый и второй вопросы следует получить формулу для вычисления силы трения. Для этого используем вторую формулу из системы (1.3) и получим:

$F_{tr}=m{\omega }^2R{\sin \varphi } \cos \varphi =\frac{1}{2}m{\omega }^2R{\sin (2\varphi )} } \qquad (2.1)$

Из формулы (2.1) следует, что сила трения равна нулю на полюсах и экваторе. Максимальную величину сила трения имеет при $\varphi =\pm \frac{\pi }{4}$ , то есть ${\sin (2\varphi )} =1.$

Рассмотрим выражение, полученное для вычисления веса тела:

$P=mg-m{\omega }^2R\cos \varphi } \qquad (2.2)$

Из него следует, что $P=mg$ при $\varphi =\frac{\pi }{2}$ , то есть на полюсах.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Формула силы инерции

Определение и формула силы инерции

Системы отсчета, движущиеся прямолинейно с постоянным ускорением

Вращающаяся система отсчета

Примеры решения задач по теме «Сила инерции»