Формула равноускоренного движения
Если скорость тела уменьшается со временем на ту же величину, то движение называют равнозамедленным.
В целом равнопеременным движением называют такое движение тела, при котором ускорение является постоянным.
Примером равноускоренного движения может быть движение тела в поле постоянного земного притяжения при условиях, когда сопротивлением воздуха можно пренебречь.
![Rendered by QuickLaTeX.com \[ a = \frac{V-V_{0}}{t} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e2d50178b68e378767e2a3c887205ad6_l3.png)
где ![]() — ускорение (определяется в м/с
— ускорение (определяется в м/с![]() ),
), ![]() — конечная скорость,
— конечная скорость, ![]() — начальная скорость,
— начальная скорость, ![]() — время.
— время.
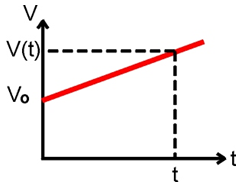
Формулы скорости и пути для ускоренного движения:
1. При одномерном равноускоренном движении скорость тела изменяется со временем линейно по закону:
![]()
2. Формула координаты тела:
![]()
3. Формула пути:
![]()
4. Формула пути, если t неизвестно:
![]()
Примеры решения задач по теме «Равноускоренное движение»
| Задание | Автомобиль, двигавшийся со скоростью 72 км/час, затормозил за 5 с. Определить ускорение равнозамедленного движения. |
| Решение | Обозначим: Переведем скорость в метры в секунду:
|
| Ответ | Ускорение равнозамедленного движения составляет |
| Задание | Перемещение тела при равноускоренном движении за первые два равные и последовательные интервалы времени по 2 с каждый соответственно равны 12 м и 32 м. Найти начальную скорость и ускорение тела. |
| Решение | Обозначим: 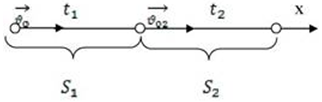
Конечная скорость, приобретенная на промежутке Учитывая Подставив (3) в (2), получим: Откуда: Теперь подставим последнюю формулу в (1): тогда
|
| Ответ | Начальная скорость равна 1 (м/с), ускорение 5 (м/с |






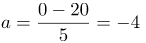 (м/с
(м/с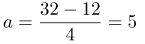 (м/с
(м/с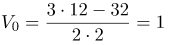 (м/с)
(м/с)





