Формула равнодействующей силы

В соответствии с первым законом Ньютона в инерциальных системах отсчета тело может изменять свою скорость только, если на него действуют другие тела. Количественно взаимное действие тел друг на друга выражают с помощью такой физической величины, как сила ( $\overline{F}$ ). Сила может изменять скорость тела, как по модулю, так и по направлению. Сила является векторной величиной, у нее есть модуль (величина) и направление. Направление равнодействующей силы определяет направление вектора ускорения тела, на которое действует рассматриваемая сила.

Основной закон, при помощи которого определяют направление и величину равнодействующей силы – это второй закон Ньютона:

$\overline{F}=m\overline{a}\ \qquad(1)$

где m – масса тела, на которое действует сила $\overline{F}$ ; $\overline{a}$ – ускорение, которое сила $\overline{F}$ сообщает рассматриваемому телу. Сущность второго закона Ньютона состоит в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Необходимо помнить, что второй закон Ньютона работает для инерциальных систем отсчета.

В том случае, если на тело действует несколько сил, то их совместное действие характеризуют при помощи равнодействующей силы. Допустим, что на тело действует одновременно несколько сил, при этом тело перемещается с ускорением, равным векторной сумме ускорений, которые появились бы при воздействии каждой из сил в отдельности. Силы, действующие на тело, и приложенные к одной его точке необходимо складывать по правилу сложения векторов. Векторная сумма всех сил, действующих на тело в один момент времени, называется равнодействующей силой ( $\overline{F}$ ):

$\overline{F}={\overline{F}}_1+{\overline{F}}_2+\dots +{\overline{F}}_N=\sum^N_{i=1}{{\overline{F}}_i}\ \qquad(2)$

Выражение (2) можно считать формулой для вычисления равнодействующей силы. Равнодействующая сила – это гипотетический (искусственный) параметр, который вводят для того, чтобы удобнее было производить расчеты.

При действии на тело нескольких сил, второй закон Ньютона записывают как:

$\sum^N_{i=1}{{\overline{F}}_i}=m\overline{a} \qquad(3)$

Равнодействующая всех сил, действующих на тело, может быть равна нулю, в том случае, если происходит взаимная компенсация сил, приложенных к телу. В таком случае тело движется с постоянной скоростью или находится в покое.

При изображении сил, действующих на тело, на чертеже, в случае равноускоренного перемещения тела, равнодействующую силу, направленную по ускорению следует изображать длиннее, чем противоположно ей направленную силу (сумму сил). В случае равномерного движения (или покоя) дина векторов сил, направленных в противоположные стороны одинакова.

Для нахождения равнодействующей силы, следует изобразить на чертеже все силы, которые необходимо учитывать в задаче, действующие на тело. Складывать силы следует по правилам сложения векторов.

Примеры решения задач по теме «Равнодействующая сила»

ПРИМЕР 1

Задание

Небольшой шарик висит на нити, он находится в покое. Какие силы действуют на данный шарик, изобразите их на чертеже. Чему равна равнодействующая сила, приложенная к телу?

Решение

Сделаем рисунок.

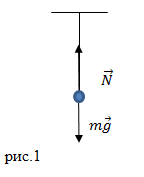
Рассмотрим систему отсчета связанную с Землей. В нашем случае эту систему отсчета можно считать инерциальной. На шарик, подвешенный на нити действуют две силы: сила тяжести, направленная вертикально вниз ( $m\overline{g}$ ) и сила реакции нити (сила натяжения нити): $\overline{N}$ . Так как шарик находится в состоянии покоя, то сила тяжести уравновешивается силой натяжения нити:

$m\overline{g}+\overline{N}=0\ \qquad(1.1)$

Выражение (1.1) соответствует первому закону Ньютона: равнодействующая сила, приложенная к телу, находящемуся в покое в инерциальной системе отсчета равна нулю.

Ответ

Равнодействующая сила, приложенная к шарику равна нулю.

ПРИМЕР 2

Задание

На тело действуют две силы и $F_1=A{\cos (\omega t)}$ и $F_2=B{\sin (\omega t)}$ , где $A,\ B,\ \omega$ – постоянные величины. ${\overline{F}}_1\bot {\overline{F}}_2$ . Чему равна равнодействующая сила, приложенная к телу?

Решение

Сделаем рисунок.

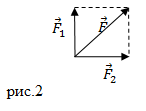
Так как векторы силы ${\overline{F}}_1$ и ${\overline{F}}_2$ перпендикулярные по отношению друг к другу, следовательно, длину равнодействующей найдем как: