Формула инерции

ОПРЕДЕЛЕНИЕ

Инерцией называют свойство тела не изменять без причины свое состояние покоя или равномерного и прямолинейного движения.

В переводе с латыни инерция обозначает косность, вялость. В инерциальных системах отсчета тело стремится сохранить свое состояние покоя или равномерного прямолинейного движения без изменения, если на него не действуют другие тела или их действие взаимно компенсируется. Инерция – это свойство материи.

Мерой инерции служит масса. При вращательном движении в качестве меры инерции часто используют момент инерции.

Масса тела

Масса является основной динамической характеристикой тела, выступает в качестве количественной характеристики его инертности, то есть возможности тела иметь определенное ускорение, которое придает ему сила. При этом для рассматриваемого тела ускорение ( $\overline{a}$ ) прямо пропорционально силе ( $\overline{F}$ ), а коэффициент пропорциональности в данном случае это масса (m):

$m\overline{a}=\overline{F} \qquad(1)$

И так, инертной массой называют физическую величину, равную частному от деления величины силы на модуль ускорения тела:

$m=\frac{F}{a} \qquad(2)$

На сегодняшний момент пока нет четкого понимания, почему тела обладают массами, в чем состоит природа массы. Почему элементарные частицы обладают теми или иными массами. Однако определение массы в виде (2) дает возможность ее измерять. Кроме того, по найденной величине массы можно точно рассчитать движение того или иного тела. В чем и состоит основная задача механики.

Масса связана с таким параметром как количество вещества ( $\nu$ ):

$m=\nu \mu \ \qquad(3)$

где $\mu$ – молярная масса вещества.

При изучении движения тела следует учитывать не только совокупную массу тела, но и распределение масс в нем.

Следует заметить, что отношение силы к ускорению тела (2) , то есть масса, является постоянной величиной при относительно небольших скоростях. Если скорость тела увеличивается, то масса растет:

$\ m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}} \qquad(4)$

где m – релятивистская масса (или просто масса); $m_0$ – масса покоя; v – скорость движения тела; c – скорость света.

Момент инерции тела

Инерцию тела во вращательном движении принято характеризовать при помощи такой физической величины как момент инерции тела (J). Момент инерции является скалярной (в общем случае тензорной) физической величиной, которую находят как сумму произведений масс материальных точек ( $\Delta m_i$ ) (на которые следует провести разбиение рассматриваемого тела) на квадраты расстояний ( $r^2_i$ ) от них до оси вращения:

$J=\sum^k_{i=1}{{\Delta m}_ir^2_i}\qquad (4)$

Подробнее о моменте инерции можно прочитать в разделах «Момент инерции тела», «Момент инерции материальной точки», «Момент инерции, единицы измерения».

Закон инерции

Закон инерции, который мы знаем, сформулировал И. Ньютон: Каждое тело находится в состоянии покоя или движется равномерно и прямолинейно, относительно любой инерциальной системы отсчета, до того момента пока действие на него других тел не заставит его изменить свое состояние.

Закон инерции является важным и независимым законом. Он отображает возможность определить пригодность системы отсчета для рассмотрения движения в динамическом и кинематическом смыслах. Он стал первым шагом при установлении основных законов классической механики.

Движение по инерции является обязательно равномерным и прямолинейным. Инерциальное движение – это движение по кратчайшему расстоянию, а кратчайшим расстоянием между двумя точками в свободном пространстве является прямая. Такое движение можно считать аналогичным покою, так как всегда можно выбрать такую инерциальную систему отсчета, которая бы перемещалась со скоростью рассматриваемого тела и в ней тело будет покоиться.

Примеры решения задач по теме «Инерция»

ПРИМЕР 1

Задание

Объясните, как связано явление инерции и брошенное тело. При каких условиях брошенный камень будет двигаться с постоянной скоростью бесконечно долго?

Решение

Так как существует явление инерции, то брошенные тела движутся. В момент броска мы сообщаем камню скорость. На тело, при его движении действует сопротивление воздуха (если бросок совершён в воздухе) и сила притяжения Земли. Если бы этих сил не было, то камень бы двигался равномерно и прямолинейно, сохраняя скорость, которую мы ему придали без изменения по величине и направлению. Именно взаимодействие камня с Землей и средой (воздухом) ведет к уменьшению скорости движения тела, к искривлению его траектории и, в конце концов, остановке.

ПРИМЕР 2

Задание

В некоторой системе отсчета имеется две одинаковые частицы (рис.1). Одна из которых покоится, другая перемещается в направлении первой частицы со скоростью 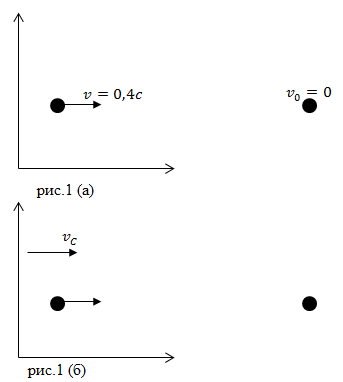$v=0,4c$ . Какова масса движущейся частицы в системе отсчета указанной в условии задачи? Какова масса частиц в системе отсчета, связанной с центром инерции системы частиц? Масса покоя частиц $m_0.$

Решение

а) Рассмотрим первый случай. Система отсчета покоится. Движется одна частица (рис.1(а)). Масса покоя частиц равна $m_0$ . Частица с нулевой скоростью свою массу не изменит. Масса частицы, перемещающейся со скоростью близкой к скорости света равна:

$m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}} \qquad(2.1)$