Формула индукции

В этом разделе мы рассмотрим только три вида индукции: электромагнитную индукцию, индукцию магнитного поля и электрическую индукцию и основные формулы, при помощи которых данные виды индукции вычисляют.

Формула индукции электрического поля

Электрическая индукция (или вектор электрического смещения ( $\overline{D}$ )) – это одна из основных векторных характеристик электрического поля. Формулой определяющей вектор электрической индукции является выражение:

$\overline{D}={\varepsilon }_0\overline{E}+\overline{P} \qquad(1)$

где $\overline{E}$ – вектор напряженности электрического поля; $\overline{P}$ – вектор поляризации; ${\varepsilon }_0$ – электрическая постоянная.

Для изотропного вещества индукция электрического поля связана с напряженность это поля как:

$\overline{D}={\varepsilon }_0\varepsilon \overline{E} \qquad(2)$

где $\varepsilon$ – диэлектрическая проницаемость вещества.

Самой распространённой формулой, при помощи которой находят величину вектора индукции электростатического поля, является теорема Остроградского – Гаусса:

$\Psi_D=\oint_S{\overline{D}d\overline{S}=\oint_S{D_ndS}=Q} \qquad (3)$

Поток ( $\Psi_D$ ) вектора электростатической индукции ( $\overline{D}$ ) в диэлектрике через произвольную замкнутую поверхность равен сумме свободных зарядов, которые находятся внутри рассматриваемой поверхности. В данной форме теорема Гаусса выполняется и для однородной и изотропной среды, так и для неоднородной анизотропной.

Формула вектора индукции магнитного поля

Модуль вектора $\overline{B}$ равен частному от деления максимальной силы Ампера ( $F_{max}$ ), с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника ( $\Delta l$ ):

$B=\frac{F_{max}}{I\Delta l} \qquad(4)$

На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца. По величине ее воздействия на заряд также можно установить модуль вектора $\overline{B}$ :

$B=\frac{F_L}{qv\sin \alpha \ } } \qquad(5)$

где $F_L$ – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; $\alpha$ – это угол между векторами $\overline{v}$ и $\overline{B}$ . Направления ${\overline{F}}_L$ , векторов $\overline{v}$ и $\overline{B}$ связаны между собой правилом левой руки.

Формулой, которая определяет величину вектора магнитной индукции в конкретной точке магнитного поля можно считать следующее выражение:

$B=\frac{M_{max}}{p_m} \qquad(6)$

где $M_{max}$ – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом $p_m$ , равным единице, если нормаль к рамке перпендикулярна направлению поля.

Основными законами, которыми пользуются чаще всего для расчета магнитных полей, являются: закон Био-Савара-Лапласа и теорема о циркуляции вектора магнитной индукции.

Формула электромагнитной индукции

Если проводник помещен в переменное магнитное поле, то в нем возникает электродвижущая сила – это сущность явления электромагнитной индукции.

Основной закон электромагнитной индукции состоит в следующем: ЭДС электромагнитной индукции ( $\varepsilon_i$ ) в контуре, помещенном в переменное магнитное поле, равна по величине скорости изменения магнитного потока ( $\Psi_m$ ), который проходит через поверхность, которую ограничивает рассматриваемый контур. При этом знаки ЭДС и скорости изменения магнитного потока противоположны.

В системе международных единиц (СИ) закон электромагнитной индукции записывают так:

$\varepsilon_i=-\frac{d\Psi_m}{dt} \qquad(7)$

где $\frac{d\Psi_m}{dt}$ – скорость изменения магнитного потока сквозь площадь, которую ограничивает контур. (Часто индекс у магнитного потока опускают и обозначают его Ф). Когда вычисляют ЭДС индукции и магнитный поток, учитывают то, что направление нормали к плоскости контура ( $\overline{n}$ ) и направление его обода связаны. Вектор $\overline{n}$ должен быть направлен так, чтобы из его конца обход контура проходил против часовой стрелки.

Примеры решения задач по теме «Индукция»

ПРИМЕР 1

Задание

Однородное электрическое поле имеет напряжённость 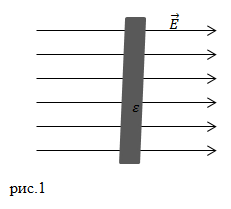$E_0$ . В него помещают бесконечную плоскопараллельную пластину из однородного изотропного диэлектрика с диэлектрической проницаемостью $\varepsilon$ . Платину размещают перпендикулярно линиям поля (рис.1). Какова напряженность (E) и индукция поля (D) внутри диэлектрика?

Решение

Напряженность электростатического поля внутри пластины будет равно:

$\overline{E}=\frac{{\overline{E}}_0}{\varepsilon }\ \qquad(1.1)$

В изотропном веществе индукция электрического поля связана с напряженность это поля как:

$\overline{D}={\varepsilon }_0\varepsilon \overline{E} \qquad(1.2)$

используя выражение (1.1), получим:

$\overline{D}={\varepsilon }_0\varepsilon \frac{{\overline{E}}_0}{\varepsilon }={\varepsilon }_0{\overline{E}}_0$

Ответ

$\overline{E}=\frac{{\overline{E}}_0}{\varepsilon };\overline{D}={\varepsilon }_0{\overline{E}}_0$

ПРИМЕР 2

Задание

Прямолинейный металлический стержень движется с постоянной скоростью v в однородном магнитном поле B. Чему будет равна разность потенциалов на концах проводника (U)? Угол между векторами 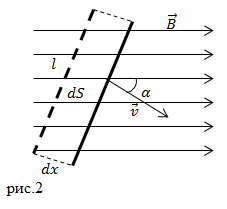$\overline{B}$ и $\overline{v}$ равен $\alpha$ .

Решение

На концах стержня при его движении появляются индуцированные заряды. Разделение зарядов в таком проводнике идет за счет магнитных сил, оказывающих воздействие на электроны. Полное разделение зарядов идет до момента пока возникшее электрическое поле не уравновешивает в любой точке стержня действие магнитного поля на заряды. Магнитные силы можно считать сторонними. Используем закон Фарадея:

$\left|\varepsilon_i\right|=\frac{d\Psi_m}{dt} \qquad(2.1)$