Формула адиабатического расширения

Формула первого начала термодинамики для адиабатического расширения

ОПРЕДЕЛЕНИЕ

Адиабатическим расширением называют процесс увеличения объема термодинамической системы без обмена теплотой с внешней средой $(\Delta Q=0)$ .

Одной из формул адиабатического расширения можно назвать запись первого начала термодинамики для данного процесса:

$A=-\Delta U\ \qquad(1)$

При адиабатном расширении газ совершает работу (расширяется, увеличивает свой объем) за счет уменьшения внутренней энергии. Для идеального газа первое начало термодинамики (адиабатический процесс), можно представить как:

$\delta A+dU=pdV+\frac{i}{2}R\nu dT\to pdV=-\frac{i}{2}R\nu dT\ \qquad(2)$

где i- число степеней свободы молекулы газа; $\nu$ – число молей вещества; $dT$ – элементарное изменение температуры; $dV$ – малое изменение объема. Из выражения (2) очевидно, что при адиабатическом расширении $(dV>0)$ газ охлаждается $(dT<0).$

Теплоемкость при адиабатическом расширении для любой термодинамической системы является постоянной и равна нулю.

Формула адиабаты для идеального газа

Адиабатическое увеличение объема в идеальном газе можно описывать применяя уравнение Менделеева – Клапейрона или иные формы уравнения состояния идеального газа. Однако, существуют специальные уравнения, которые дают возможность описать рассматриваемый нами процесс двумя параметрами:

$f\left(p,V\right);\ f\left(p,T\right);\ f\left(V,T\right)$

Такие формулы называют уравнениями Пуассона:

$pV^{\gamma }=const;\ TV^{\gamma -1}=const;\ pT^{\frac{\gamma }{\gamma -1}}=const\ \qquad(3)$

где $\gamma =\frac{i+2}{i}$ — показатель адиабаты (коэффициент Пуассона); i – число степеней свободы молекулы газа. Или, что то же самое:

$\frac{p_2}{p_1}={\left(\frac{V_1}{V_2}\right)}^{\gamma };\ \frac{T_2}{T_1}={\left(\frac{V_1}{V_2}\right)}^{\gamma -1};\ \frac{T_2}{T_1}={\left(\frac{p_2}{p_1}\right)}^{\frac{\gamma -1}{\gamma }} \qquad(4)$

Энтропия в адиабатическом процессе

Равновесный адиабатический процесс часто характеризуют при помощи такой физической величины как энтропия (S). В равновесном процессе этот термодинамический параметр определяют как:

$dS=\frac{\delta Q}{T} \qquad(5)$

Из формулы (5) следует, что равновесный адиабатический процесс является изоэнтропийным (энтропия не изменяется), то есть в таком процессе:

$\Delta S=0\to S=const\ \qquad(6)$

Выражение (6) – это еще одна формула, которую можно использовать при рассмотрении процесса адиабатического расширения.

Формула для работы газа при адиабатическом расширении

При адиабатическом расширении газ совершает работу за счет уменьшения своей внутренней энергии:

$A=-\frac{i}{2}\nu R\left(T_2-T_1\right)=-\Delta U\ \qquad(7)$

где i – число степеней свободы молекулы газа; $\nu =\frac{m}{\mu }$ – количество вещества; $\mu$ – молярная масса газа.

Расчёт работы, которую выполняет идеальный газ в процессе адиабатического расширения можно вычислить, если знать начальную температуру газа ( $T_1$ ) и начальный ( $V_1$ ) и конечный его объемы ( $V_2$ ):

$A=\frac{i}{2}\frac{m}{\mu }RT_1\left(1-\frac{V^{\gamma -1}_1}{V^{\gamma -1}_2}\right) \qquad(8)$

Примеры решения задач по теме «Адиабатическое расширение»

ПРИМЕР 1

Задание

В результате обратимого адиабатического расширения температура $m=$ 1 кг азота ( $N_2$ ) снижается на $\Delta T=T_1-T_2=$ 20 К. Какова работа, которую совершает газ в этом процессе, если считать, что колебательные степени свободы молекул можно не учитывать?

Решение

В качестве основы для решения задачи используем формулу для вычисления работы в адиабатическом расширении в виде:

$A=-\frac{i}{2}\nu R\left(T_2-T_1\right)=\frac{i}{2}\nu R\Delta T \qquad(1.1)$

где $\nu =\frac{m}{\mu }$ . Молярная масса азота равна: ${\mu }_{N_2}=28\cdot {10}^{-3}\frac{kg}{mol}$ . Число степеней свободы у молекулы, состоящей из двух атомов, если колебательные степени свободы можно не принимать в расчет, равно $i=5$ .

Вычислим работу, которую совершает газ:

$A=\frac{5}{2}\cdot \frac{1}{28\cdot {10}^{-3}}\cdot 8,31\cdot 20=14,83\cdot {10}^3(J)$

Ответ

$A=14,83\cdot {10}^3$ Дж

ПРИМЕР 2

Задание

Изобразите на диаграмме U(S) график адиабатного и изотермического расширения идеального газа.

Решение

Рассмотрим процесс адиабатического расширения. Адиабатическое расширение идеального газа происходит без изменения энтропии:

$\Delta S=0\to S=const\ \qquad(2.1)$

Это означает, что прямая, изображающая адиабатный процесс (адиабата) будет перпендикулярна оси S.

При адиабатном расширении внутренняя энергия идеального газа уменьшается. Объем газа увеличивается, газ совершает работу за счет уменьшения внутренней энергии газа:

$A=-\Delta U\ \qquad(2.2)$

Это отразим на графике (рис.1) прямая АВ.

Рассмотрим изотермический процесс (T=const). В изотермическом процессе изменения внутренней энергии газа не происходит, так как $\Delta T=0$ . Изотерма будет прямой линией, перпендикулярной оси U. В изотермическом расширении энтропия растет, так как:

$\Delta S=\nu Rln\left(\frac{V_2}{V_1}\right)\ \qquad(2.3)$

Изотермический процесс на графике рис.1 изображает прямая CD.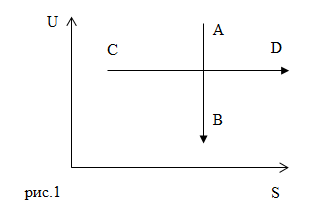

Понравился сайт? Расскажи друзьям!

Советуем прочитать: