Условия максимума и минимума интерференции

Общие сведения об интерференции

Допустим, что для получения когерентных волн мы используем один источник света, и применяем метод разделения волны на две части, деление происходит в некоторой точке О. Данные волны проходят разные световые пути. Одна волна проходит путь $s_1$ в веществе с показателем преломления $n_1$ , другая – $s_2$ , при этом показатель преломления среды $n_2$ . В некоторой точке М волны накладываются друг на друга и создают интерференционную картину. Фазу колебаний в волне для точки О обозначим $\omega t$ , тогда в точке М первая волна возбуждает колебания: $A_1{\cos (\omega t-\frac{s_1}{v_1})}$ ; вторая волна в точке М создает колебания: $A_2{\cos (\omega t-\frac{s_2}{v_2})}$ . Причем известно, что фазовые скорости рассматриваемых волн равны:

$v_1=\frac{c}{n_1};\ \ v_2=\frac{c}{n_2} \qquad (1),$

где c – скорость света в вакууме. При этом разность фаз колебаний ( $\delta$ ), которые возбуждаются волнами в точке М:

$\delta =\omega \left(\frac{s_2}{v_2}-\frac{s_1}{v_1}\right)=\frac{2\pi} {{\lambda}_0}\left(s_2n_2-s_1n_1\right) \qquad (2),$

где ${\lambda}_0$ – длина волны в вакууме; $\omega =\frac{2\pi}{\lambda_0} c$ . Обозначим величину $s\cdot n=L$ , и назовем ее оптической длиной пути L. При этом разность ( $\Delta$ ):

$\Delta =L_2-L_1 \qquad (3),$

называют оптической разностью хода.

Условия максимума и минимума интерференции

В том случае, если оптическая разность хода будет равна целому числу длин волн в вакууме, то в данной точке наблюдается максимум интенсивности. Колебания, которые создаются двумя волнами, которые мы рассматривали в точке М, происходят в одной фазе. Условия интерференционного максимума можно записать как:

$\Delta =\pm m \lambda_0 \qquad (4),$

где m – целое число, начинающееся с нуля. При этом $\delta =\pm 2\pi m$ .

Когда оптическая разность хода разна нечетному числу длин полуволн, то в исследуемой точке наблюдают интерференционный минимум. В виде формулы, условие интерференционного минимума записывают:

$\Delta =\pm (2m+1)\frac{{\lambda}_0} {2} \qquad (5),$

где ${\rm m}$ – целое число с нуля. При этом разность фаз суммирующихся волн в точке равна $\delta {\rm =\pm} \pi {\rm (2}{\rm m}{\rm +1).}$ Колебания в точке М наших волн происходят в противофазе. Выражение (5) есть условие интерференционного минимума.

Примеры решения задач

ПРИМЕР 1

Задание

Оптическая разность хода ( $\Delta$ ) двух волн при интерференции монохроматического света оказалась равна $0,3\ {\lambda}_0$ . Какова разность фаз ( $\delta$ ) при этом?

Решение

За основу решения задачи примем формулу:

$\delta =\frac{2\pi} {{\lambda}_0}\left(s_2n_2-s_1n_1\right) \qquad (1.1),$

где $s_2n_2-s_1n_1=L_2-L_1=\Delta$ , то есть связь между разностью фаз и разностью хода реализуется при помощи формулы:

$\delta =\frac{2\pi} {{\lambda}_0}\Delta$

Можно вычислить искомую разность фаз:

$\delta =\frac{2\pi} {{\lambda}_0}\cdot 0,3\ {\lambda}_0=0,6\pi \approx 1,88$

Ответ

$\delta =1,88$

ПРИМЕР 2

Задание

Вычислите, на каком расстоянии от точки А (рис.1) будут находиться первые максимумы освещенности на экране, если 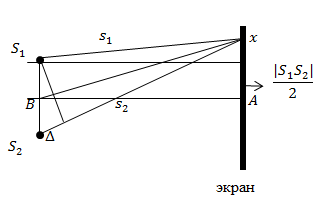$S_1$ и $S_2$ – когерентные источники света с длиной волны ${\lambda}_0=6\cdot {10}^{-7}$ м. Расстояние ВА равно 4 м, расстояние между источниками равно 1 мм. На каком расстоянии от точки А находятся вторые минимумы интерференции?

Условия максимума и минимума интерференции, пример 1

Рис. 1

Решение

В качестве основы для решения задачи используем условие максимума интерференции:

$\Delta =\pm m{\lambda}_0 \qquad (2.1),$

так как нам по условию задачи требуется найти расстояние от точки A то первого максимума, то $m=1,$ следовательно, выражение (2.1) преобразуется к виду:

$\Delta =\pm {\lambda}_0 \qquad (2.2)$

Из уравнения (2.2) следует, что первых максимумов интерференции будет два, по обе стороны от точки А. Из рис.1 найдем разность хода двух волн ( $\Delta$ ), как:

$\Delta =s_2-s_1 \qquad (2.3)$

Рассматривая треугольники на рис.1 мы имеем:

${s_2}^2={\left|AB\right|}^2+{\left(x+\frac{\left|S_1S_2\right|}{2}\right)}^2;\ {s_1}^2={\left|AB\right|}^2+{\left(x-\frac{\left|S_1S_2\right|}{2}\right)}^2\ \to {s_2}^2-{s_1}^2=2x\frac{\left|S_1S_2\right|}{2} \qquad (2.4)$

Используя выражения (2.3) и (2.4), имеем:

$\Delta =s_2-s_1=2x\frac{\left|S_1S_2\right|}{2\left(s_2+s_1\right)} \qquad (2.5)$

$\Delta =\frac{x\left|S_1S_2\right|}{\left|AB\right|} \qquad (2.6)$

Используем условие максимума (2.2) и формулу (2.6):

$\frac{x_{max1}\left|S_1S_2\right|}{\left|AB\right|}=\pm {\lambda}_0 \qquad (2.7)$

Из выражения (2.7) получим формулу для вычисления искомого расстояния (x):

$x_{max1}=\pm \frac{|AB|}{\left|S_1S_2\right|}{\lambda}_0$

Можно провести вычисления:

$x_{max1}=\pm \frac{4}{{10}^{-3}}\cdot 6\cdot {10}^{-7}=\pm 2,4\cdot {10}^{-3}(m)$

Для ответа на второй вопрос задачи: «На каком расстоянии от точки А находятся вторые минимумы интерференции?» используем условие минимума:

$\Delta =\pm \left(2m+1\right)\frac{{\lambda}_0} {2} \qquad (2.8),$

где m=2, тогда выражение (287) примет вид:

$\Delta =\pm \left(2\cdot 2+1\right)\frac{{\lambda}_0} {2}=\pm \frac{5} {2}{\lambda}_0 \qquad (2.9)$

Приравняем правые части выражений (2.9) и (2.6), получаем:

$\frac{x_{min2}\left|S_1S_2\right|}{\left|AB\right|}=\pm \frac{5} {2}{\lambda}_0\ \left(2.10\right)$

Тогда выражение для вычисления вторых интерференционных минимумов:

$x_{min2}=\pm \frac{5} {2} \lambda_0\ \frac{\left|AB\right|}{\left|S_1S_2\right|}$

Проведем вычисления $x_{min2}$ :

$x_{min2}=\pm \frac{5} {2}\cdot 6 \cdot {10}^{-7}\cdot \ \frac{4}{{10}^{-3}}=\pm 6 \cdot {10}^{-3}(m)$

Ответ

1) $x_{max1}=\pm 2,4\cdot {10}^{-3}$ . 2) $x_{min2}=\pm 6\cdot {10}^{-3}$ м

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Условия максимума и минимума интерференции

Общие сведения об интерференции

Условия максимума и минимума интерференции

Примеры решения задач