Тензор деформации

Определение и общие понятия деформации

Если к твердому телу приложен сила, то оно деформируется, то есть изменяет свою форму и объем. Для того чтобы описать деформацию тела положение его каждой точки определяют при помощи радиус-вектора $\overline{r}$ , имеющего в некоторой системе координат компоненты: $x=x_1,y=x_2,z=x_3\ (x_i).$ При деформации тела все его точки смещаются. Пусть положение какой –то определенной точки тела до деформации определялось вектором $\overline{r}$ , то в деформированном теле положение ее же определит другой вектор $\overline{r}'$ , имеющий компоненты $x_i'$ . Смещение рассматриваемой точки тела определит вектор:

${\overline{r}}'-\overline{r}=\overline{u} \qquad (1)$

вектор $\overline{u}$ называют вектором деформации (вектором смещения). При этом координаты $x_i'$ являются функциями от координат $x_i,$ следовательно, вектор $\overline{u}$ является функцией координат $x_i$ . Если задан вектор смещения, то считают, что о полностью определяет деформацию.

При деформировании тела изменяются расстояния между его точками. Рассмотрим две близкие точки тела. Если радиус-вектор между ними до деформирования был ${dx}_i$ , то в теле подвергшемся деформации радиус-вектор между теми же точками ( ${dx}_i'$ ) равен:

${dx}'_i={dx}'_i+du_i \qquad (2)$

Расстояние ( $dl$ ) между рассматриваемыми точками до деформации равно:

$dl=\sqrt{dx^2_1+dx^2_2+dx^2_3}\to dl^2=dx^2_i \qquad (3)$

После деформации расстояние между теми же точками ( $dl'$ ) равно:

$dl'=\sqrt{{dx'}^2_1+d{x'}^2_2+{dx'}^2_3}\to {dl'}^2=dx^{'2}_i={\left(dx_i+du_i\right)}^2 \qquad (4)$

Учтем, что:

$du_i=\frac{\partial u_i}{\partial x_k}dx_k \qquad (5)$

${dl'}^2$ преобразуем к виду:

${dl'}^2=dl^2+2\frac{\partial u_i}{\partial x_k}dx_idx_k+\frac{\partial u_i}{\partial x_k}\frac{\partial u_i}{\partial x_m}dx_idx_m \qquad (6)$

Так как во втором члене индексы i; k являются немыми, то это слагаемое можно записать в симметричном виде, как:

$\left(\frac{\partial u_i}{\partial x_k}+\frac{\partial u_k}{\partial x_i}\right)dx_idx_k$

В третьем слагаемом выражения (6) поменяем местами индексы i; m в результате получим:

${dl'}^2=dl^2+2u_{ik}dx_idx_k \qquad (7)$

где

$u_{ik}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_k}+\frac{\partial u_k}{\partial x_i}+\frac{\partial u_m}{\partial x_i}\frac{\partial u_m}{\partial x_k}\right) \qquad (8)$

Тензор деформации

Выражение (7) определяет изменение элемента длины при деформации тела. Тензор $u_{ik}$ называют тензором деформации. Он обладает свойством симметрии:

$u_{ik}=u_{ki} \qquad (9)$

Как любой симметричный тензор его можно привести в каждой точке к главным осям, что означает: в каждой точке можно избрать такую систему координат, в которой все компоненты этого тензора равны нулю, кроме диагональных. Если тензор $u_{ik}$ приведен к главным осям в некоторой точке тела, то он не диагонален во всех других точках.

Если тензор деформации привели в рассматриваемой точке к главным осям, то в окружающем его элементе объема элемент длины имеет вид:

${dl'}^2=\left({\delta }_{ik}+2u_{ik}\right)dx_idx_k=\left(1+2u_{11}\right)dx^2_1+\left(1+2u_{22}\right)dx^2_2+\left(1+2u_{33}\right)dx^2_3 \qquad (10)$

В выражении (10) имеется три независимых слагаемых, что означает, в каждом элементе объема тела деформацию можно рассмотреть как систему трех независимых деформаций по трем взаимно перпендикулярным направлениям (главным осям тензора деформации). Каждая из таких деформаций является простым растяжением (сжатием) по соответствующему направлению. Длина $dx_1$ вдоль первой главной оси становится равной:

$d{x'}_1=\sqrt{1+2u_{11}}dx_1 \qquad (11)$

Для двух других осей аналогично.

В подавляющем большинстве случаев деформации являются малыми величинами. Это означает, что изменение расстояния в теле мало в сравнении с самим расстоянием (относительные удлинения малы в сравнении с единицей). Соответственно, все составляющие тензора деформации являются малыми. Вектор же деформации может быть большим, даже если деформации малы.

При малых деформациях смещения $u_i$ и их производные по координатам будут малы. Значит, в выражении (8) можно пренебречь последним слагаемым, так как он является малой величиной второго порядка. При малых деформациях тензор деформации определяют как:

$u_{ik}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_k}+\frac{\partial u_k}{\partial x_i}\right) \qquad (12)$

В таком случае относительные удлинения элементов длины по направлениям главных осей тензора деформации в точке равны (с точностью до величин высших порядков) главным значениям тензора $u_{ik}.$

Примеры решения задач

ПРИМЕР 1

Задание

Каковы компоненты вектора деформации стержня длины 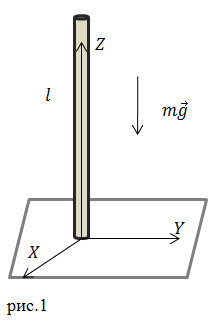$l$ , который стоит вертикально в поле тяжести (рис.1).

Решение

Ось Z направим вдоль оси стержня (рис.1), нижнее основание стержня «стоит» на плоскости XY. Запишем уравнения равновесия стержня:

$\frac{\partial {\sigma }_{xi}}{\partial x_i}=\frac{\partial {\sigma }_{yi}}{\partial x_i}=0; \ \frac{\partial {\sigma }_{zi}}{\partial x_i}=\rho g\ \qquad (1.1)$

где ${\sigma }_{xi};\ {\sigma }_{yi}; {\sigma }_{zi}$ – компоненты тензора напряжения. На боковой поверхности стержня равны нулю все составляющие ${\sigma }_{ik}$ кроме ${\sigma }_{zz}$ . На верхнем основании нашего стержня ${\sigma }_{xz}={\sigma }_{yz}={\sigma }_{zz}$ =0. Решение уравнений равновесия, которое удовлетворяет названным условиям:

${\sigma }_{zz}=-\rho g\left(l-z\right) \qquad (1.2)$

Все остальные ${\sigma }_{ik}=0.$ Зная ${\sigma }_{ik}$ определим $u_{ik}$ как:

$u_{xx}=u_{yy}=\frac{\sigma }{E}\rho g\left(l-z\right); \ u_{zz}=-\frac{\rho g\left(l-z\right)}{E}; \ u_{xy}=u_{yz}=u_{xz}=0\ (1.3)$

Интегрируя выражения (1.3) получим составляющие вектора деформации:

$u_x=\frac{\sigma }{E}\rho g\left(l-z\right)x; \ u_y=\frac{\sigma }{E}\rho g\left(l-z\right)y; \ u_z=-\frac{\rho g}{2E}\left(l^2-{\left(l-z\right)}^2-\sigma \left(x^2+y^2\right)\right)$

Формула, определяющая $u_z$ удовлетворяет граничному условию $u_z=0$ только в одной точке нижнего основания стержня, следовательно, это решение не применимо около нижнего конца стержня.

Ответ

$u_x=\frac{\sigma }{E}\rho g\left(l-z\right)x; \ u_y=\frac{\sigma }{E}\rho g\left(l-z\right)y; \ u_z=-\frac{\rho g}{2E}\left(l^2-{\left(l-z\right)}^2-\sigma \left(x^2+y^2\right)\right)$

ПРИМЕР 2

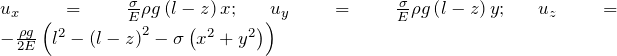
Задание

Рассмотрите бесконечно малый элемент объема ( $dV$ ) и определите его объем ( $dV'$ ) после деформации тела.

Решение

Выберем в качестве осей координат главные оси тензора деформации в точке рассмотрения. В таком случае элементы длины $dx_1,\ dx_2,\ dx_3$ по этим осям после деформации перейдут в величины:

$d{x'}_1=\left(1+u_{11}\right)dx_1; \ d{x'}_2=\left(1+u_{22}\right)dx_2; \ \ d{x'}_3=\left(1+u_{33}\right)dx_3\ \qquad (2.1)$