Радиус инерции

Осевые моменты инерции для твердых тел в некоторых случаях задают при помощи массы и радиуса инерции такого тела. Обычно радиус инерции обозначают буквой $\rho$ , но могут встречаться и другие обозначения. Для того чтобы не путать радиус инерции с плотностью вещества радиус инерции идентифицируют при помощи индекса, например пишут: ${\rho }_x$ . Особенно часто радиус инерции применяют для выражения осевых моментов инерции тел, имеющих сложную форму.

Определения радиуса инерции

ОПРЕДЕЛЕНИЕ

Радиусом инерции ( ${\rho }_x$ ) твердого тела по отношению к заданной оси X называют расстояние от оси, при этом выполняется равенство:

$J_x=m{{\rho }_x}^2 \qquad (1)$

где $J_x$ – осевой момент инерции тела; $m$ – масса тела.

Выражение (1) означает, что ${\rho }_x$ равен расстоянию от оси до места в пространстве, в котором следует сосредоточить всю массу тела для того, чтобы момент инерции данной материальной точки был равен моменту инерции тела по отношению к той же оси.

Так, например, момент инерции однородного шара массы $m$ радиуса R относительно оси X, проходящей через его центр, равен:

$J_x=\frac{2}{5}mR^2 \qquad (2)$

Момент инерции материальной точки, имеющей массу $m$ , находящейся на расстоянии ${\rho }_x$ от этой же оси равен:

$J_x=m{{\rho }_x}^2 \qquad (3)$

Приравнивая правые части выражений (2) и (3), выразим радиус инерции и для шара получим:

$\frac{2}{5}mR^2=m{{\rho }_x}^2\to {\rho }_x\approx 0,632\ R$

Используя радиус инерции, можно используя формулу (1) найти момент инерции тела и наоборот.

Радиусом инерции сечения (плоской фигуры) ( ${{\rm i}}_{{\rm x}}$ ) относительно оси X, называют величину равную:

$i_x=\sqrt{\frac{J_x}{S}} \qquad (4)$

Из выражения, определяющего радиус инерции сечения (4), следует, что он равен расстоянию от оси X до точки, в которой необходимо сосредоточить всю площадь рассматриваемого сечения (S), при этом момент инерции этой точки будет равен моменту инерции всего сечения.

Радиусы инерции, которые соответствуют главным осям, называют главными радиусами инерции. Их определяют при помощи выражений:

$i_{max}=\sqrt{\frac{J_{max}}{S}};\qquad i_{min}=\sqrt{\frac{J_{min}}{S}; } \qquad (5)$

Радиусы инерции измеряются в метрах в международной системе единиц (СИ).

Примеры решения задач

ПРИМЕР 1

Задание

Каков радиус инерции однородного цилиндра относительно оси 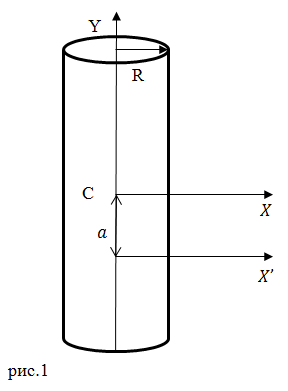$X'$ , которая перпендикулярна оси цилиндра, и находится на расстоянии $a$ от центра масс $(C).$ Радиус цилиндра равен R, его высота h.

Решение

Момент инерции однородного цилиндра относительно оси вращения, которая проходит через центр масс тела ( $J_x$ ), перпендикулярно его оси (рис.1) равен:

$J_x=\frac{1}{12}m\left(3R^2+h^2\right) \qquad (1.1)$

Используя теорему Штейнера, найдем момент инерции этого цилиндра относительно оси, параллельной оси X, находящейся на расстоянии $a$ от первой:

$J_{x'}=J_x+ma^2=\frac{1}{12}m\left(3R^2+h^2\right)+ma^2 \qquad (1.2)$

Из определения радиуса инерции имеем:

${\rho }_x=\sqrt{\frac{J_x}{m}} \qquad (1.3)$

Окончательно получаем:

${\rho }_x=\sqrt{\frac{1}{12}\left(3R^2+h^2\right)+a^2}$

Ответ

${\rho }_x=\sqrt{\frac{1}{12}\left(3R^2+h^2\right)+a^2}$

ПРИМЕР 2

Задание

Найдите радиус инерции тонкого стержня ( ${\rho }_x$ ), длина которого равна $l,$ относительно оси, перпендикулярной к стержню, проходящей через один из его концов.

Решение

Сначала найдем момент инерции (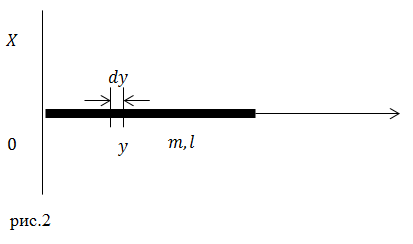 $J_x$ ) однородного тонкого стержня относительно оси, которая проходит через его конец (рис.2).

На стержне выделим материальную точку на некотором расстоянии $y$ от оси X, тогда момент инерции для этой точки запишем как:

$dJ_x=y^2dm\ \qquad (1.1)$

Так как стержень по условию однородный, то:

$dm=\tau dy\ \qquad (1.2)$

где $\tau =\frac{m}{l}$ – линейная плотность вещества стержня. Момент инерции всего стержня найдем интегрированием выражения (1.1):

$J_x=\int^l_0{y^2\tau dy}=\tau\int^l_0{y^2dy=\tau {\left.\frac{y^3}{3}\right|}^l_0}=\frac{ml^3}{l3}=\frac{ml^2}{3} \qquad (1.3)$

Для нахождения радиуса инерции воспользуемся его определением:

${\rho }_x=\sqrt{\frac{J_x}{m}} \qquad (1.4)$

Тогда получим:

${\rho }_x=\sqrt{\frac{ml^2}{3}\frac{1}{m}}=\sqrt{\frac{l^2}{3}}$

Ответ

${\rho }_x=0,577\ l$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Радиус инерции

Определения радиуса инерции

Примеры решения задач