Поток магнитной индукции

Определение и общие понятия потока магнитной индукции

ОПРЕДЕЛЕНИЕ

Потоком вектора магнитной индукции (или магнитным потоком) (dФ) в общем случае, через элементарную площадку $dS$ называют скалярную физическую величину, которая равна:

$d\Phi=\overline{B}d\overline{S}=BdS{\cos \alpha} \qquad (1)$

где $\alpha$ – угол между направлением вектора магнитной индукции ( $\overline{B}$ ) и направлением вектора нормали ( $\overline{n}$ ) к площадке dS ( $d\overline{S}=dS\overline{n}$ ).

Исходя из формулы (1), магнитный поток через произвольную поверхность S вычисляется (в общем случае), как:

$\Phi=\int_S{\overline{B}d\overline{S}} \qquad (2)$

Магнитный поток однородного магнитного поля сквозь плоскую поверхность можно найти как:

$\Phi=BS{\cos \alpha} \qquad (3)$

Для однородного поля, плоской поверхности, расположенной перпендикулярно вектору магнитной индукции магнитный поток равен:

$\Phi=BS \qquad(4)$

Поток вектора магнитной индукции может быть отрицательным и положительным. Это связано с выбором положительного направления $\overline{n}$ . Очень часто поток вектора магнитной индукции связывают с контуром, по которому течет ток. В этом случае положительное направление нормали к контуру связано с направлением течения тока правилом правого буравчика. Тогда, магнитный поток, который создается контуром с током, сквозь поверхность, ограниченную этим контуром является всегда большим нуля.

Единица измерения потока магнитной индукции в международной системе единиц (СИ) – это вебер (Вб). Формулу (4) можно использовать для определения единицы измерения магнитного потока. Одним вебером называют магнитный поток, который проходит сквозь плоскую поверхность площадь, которой 1 квадратный метр, размещенную перпендикулярно к силовым линиям однородного магнитного поля:

$\left[\Phi\right]=1Tl\cdot 1m^2$

Теорема Гаусса для магнитного поля

Теорема гаусса для потока магнитного поля отображает факт отсутствия магнитных зарядов, из-за чего линии магнитной индукции всегда замкнуты или уходят в бесконечность, у них нет начала и конца.

Формулируется теорема Гаусса для магнитного потока следующим образом: Магнитный поток сквозь любую замкнутую поверхность (S) равен нулю. В математическом виде данная теорема записывается так:

$\Phi=\oint_S{\overline{B}d\overline{S}=0\ \left(4\right).}$

Получается, что теоремы Гаусса для потоков вектора магнитной индукции ( $\overline{B}$ ) и напряженности электростатического поля ( $\overline{E}$ ), сквозь замкнутую поверхность, отличаются принципиальным образом.

Примеры решения задач

ПРИМЕР 1

Задание

Рассчитайте поток вектора магнитной индукции через соленоид, который имеет N витков, длину сердечника l, площадь поперечного сечения S, магнитную проницаемость сердечника $\mu$ . Сила тока, текущего через соленоид равна I.

Решение

Внутри соленоида магнитное поле можно считать однородным. Магнитную индукцию легко найти, используя теорему о циркуляции магнитного поля и выбрав в качестве замкнутого контура (циркуляцию вектора $\overline{B}$ по которому будем рассматривать (L)) прямоугольный контур (он будет охватывать все N витков). Тогда запишем (учитываем, что вне соленоида магнитное поле равно нулю, кроме того там, где контур L перпендикулярен линиям магнитной индукции В=0):

$\oint_L{Bdl={\mu \mu}_0NI\to B=\frac{\mu {\mu}_0NI}{l}} \qquad (1.1)$

При этом магнитный поток сквозь один виток соленоида равен ( $\Phi_1$ ):

$\Phi_1=BS \qquad (1.2)$

Полный поток магнитной индукции, который идет через все витки:

$\Phi=N\Phi_1=NBS=N^2\frac{\mu {\mu}_0I}{l}S$

Ответ

$\Phi=N^2\frac{\mu {\mu}_0I}{l}S$

ПРИМЕР 2

Задание

Каким будет поток магнитной индукции через квадратную рамку, которая находится в вакууме в одной плоскости с бесконечно длинным прямым проводником с током (рис.1). Две стороны рамки параллельны проводу. Длина стороны рамки составляет b, расстояние от одной из сторон рамки равно c.

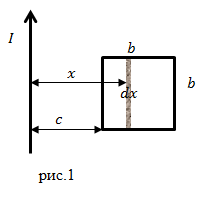
Решение

Выражение, при помощи которого можно определить индукцию магнитного поля будем считать известным (см. Пример 1 раздела «Магнитная индукция единица измерения»):

$B=\frac{{\mu}_0I}{2\pi x} \qquad (2.1)$

где x – расстояние от проводника, до точки, в которой рассматривается поле. Для нахождения искомого магнитного потока используем формулу:

$\Phi=\int_S{\overline{B}d\overline{S}} \qquad (2.2)$

где $\alpha =90^\circ$ , поэтому выражение (2.2) преобразуется к виду:

$\Phi=\int_S{BdS} \qquad (2.3)$

Выделим на плоскости рамки элементарный участок dS, его площадь равна (см. рис.1):

$dS=bdx \qquad (2.4)$

Из рис.1 видно, что $c\le x\le c+b$ . Подставим (2.1) и (2.4) в (2.3), имеем:

$\Phi=\int^{c+b}_c{\frac{{\mu}_0I}{2\pi x}}bdx=\frac{{\mu}_0Ib}{2\pi}\int^{c+b}_c{\frac{dx}{x}}=\frac{{\mu}_0Ib}{2\pi}{\ln \left(\frac{c+b}{c}\right)}$

Ответ

Ф= $\frac{{\mu}_0Ib}{2\pi}{\ln \left(\frac{c+b}{c}\right)}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Поток магнитной индукции

Определение и общие понятия потока магнитной индукции

Теорема Гаусса для магнитного поля

Примеры решения задач